We here present the system of equation corresponding to the irreversible binding TMDD model, as well as the model behavior.
Equations
If the binding of the ligand to the receptor is so strong that the dissociation of the ligand from the receptor is negligible, one can consider the binding reaction as irreversible, i.e . This approximation has been proposed in Gibiansky et al. PAGE 2010 poster, as a simplification of the full model. In this case, the system of ODEs reduces to:
with L the concentration of the ligand in plasma, R the concentration of the target/receptor, and P the concentration of the complex. V is the volume of the central compartment for the ligand, kel the linear elimination rate for the ligand, kon the binding rate, ksyn the synthesis rate for the target/receptor, kdeg its degradation rate, and kint the degradation rate of the complex. In(t) represents the input function, corresponding to the input rate (amount per unit time) of the ligand into the central compartment due to the ligand administration.
In the library model file, a slightly different parameterization is used using the steady-state initial receptor concentration (which replaces kdeg in the list of parameters). This permits to better separate the effect of each parameter.
With a second compartment, one obtains:
with A the amount of ligand in peripheral tissues, k12 the rate of transfert from central to peripheral, and k21 the rate in the opposite direction.
This approximation has one parameter less compared to the full model (koff is fixed to zero). In addition, if only the free ligand L and/or the free receptor R are observed, the equation for P can be removed, leading to:
In this case, the system has two parameters less then the full system: koff is fixed to zero and kint doesn’t influence the observed species L and R.
Model properties
We investigate the influence of each parameter on the typical free ligand concentration-time shape for several dose amounts.
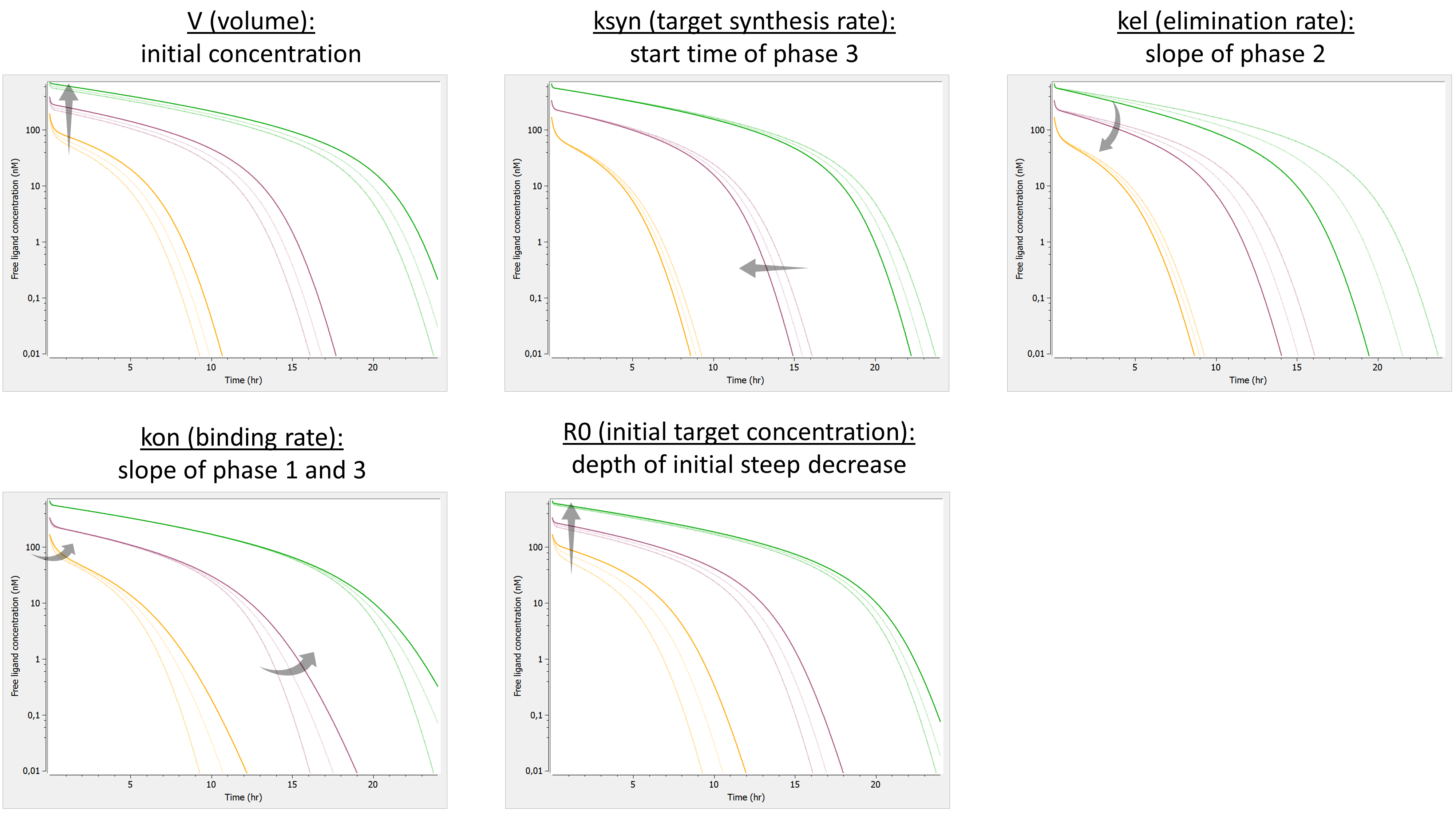
The summary picture is:
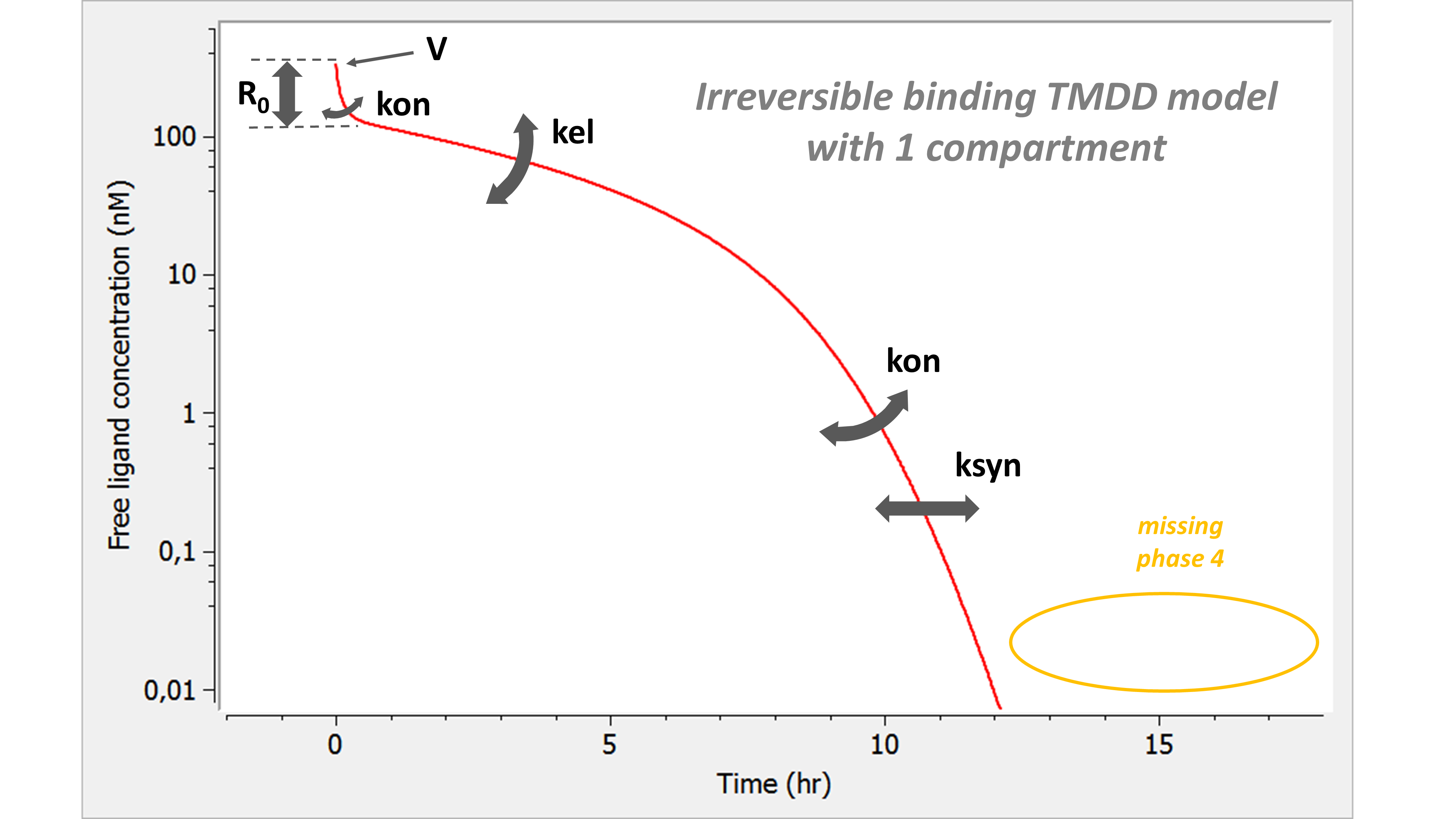
We observe that the phase 4 is completely missing. This approximation can make sense when the phase 4 is below the lower limit of quantification and no data point can be recorded in this zone. If this is the case, KD (or koff) and kint cannot be estimated. Note that if measurements about Ltot, Rtot or P would be available, then the kint parameter might be identifiable.
Model with 2 compartments
If a second compartment is added, the shape is modified in the following way. Note that kon has been chosen large (very steep phase 1), to better focus on phase 2, where k12 and k21 have their main effect.

The introduction of a second compartment permits to recover a phase 4. Its flexibility is limited and linked to the effect of parameters k12 and k21 on phase 2.
Click here to go back to main TMDD page.