Michaelis-Menten (MM) TMDD model

We here present the system of equation corresponding to the Michaelis-Menten (MM) TMDD model, as well as the model behavior.

Equations

The MM TMDD model has been proposed in Gibiansky et al. (2008), JPP 35(5). It is a further simplification of the Wagner model, assuming that \frac{R_0K_D}{(L+K_D)^2}\ll1. Introducing K_m=K_D and V_m=k_{\textrm{int}}R_0 (which reduces by one the number of parameters), the equation for the free ligand reads:

\dfrac{dL}{dt} =  \dfrac{\textrm{In}(t)}{V} - k_{\textrm{el}} \: L - \dfrac{V_m\:L}{K_D+L}

with L the concentration of the ligand in plasma. V is the volume of the central compartment for the ligand, kel the linear elimination rate for the ligand, Vm the maximal velocity of the non-linear elimination and Km the Michaelis-Menten constant of the non-linear elimination. In(t) represents the input function, corresponding to the input rate (amount per unit time) of the ligand into the central compartment due to the ligand administration.

With a second compartment, the model becomes:

\begin{array}{ccl} \dfrac{dL}{dt} &=&  \dfrac{\textrm{In}(t)}{V} - k_{\textrm{el}} \: L - \dfrac{V_m\:L}{K_D+L} - k_{\textrm{12}}\:L + k_{\textrm{21}}\:A/V \\ \dfrac{dA}{dt} &=& k_{\textrm{12}}\:L\:V - k_{\textrm{21}}\:A \end{array}

with A the amount of ligand in peripheral tissues, k12 the rate of transfert from central to peripheral, and k21 the rate in the opposite direction.

The MM model can also be derived from the “irreversible + constant Rtot” model, assuming a quasi state-steady on P (i.e k_{\textrm{on}}L(R_0-P)-k_{\textrm{int}}P=0) and \frac{R_0K_I}{(L+K_I)^2}\ll1 with K_I=\frac{k_{\textrm{int}}}{k_{\textrm{on}}}.

In principle, a dose correction must also be applied in case of bolus administration, to split the incoming drug amount into free and bound ligand. However, the dose correction requires the use of one additional parameter, which would cancel out the advantages of the MM model compared to the Wagner or “constant Rtot + irreversible binding” models. Similarly, the concentrations of P, R, Rtot and Ltot could be calculated from the concentration of L, but this would require to use of R0 as additional parameter. The MM model with 4 parameters (6 if 2 compartments) is thus applicable only if the only measured species is the free ligand.

Model properties

We investigate the influence of each parameter on the typical free ligand concentration-time shape for several dose amounts (bolus administration).

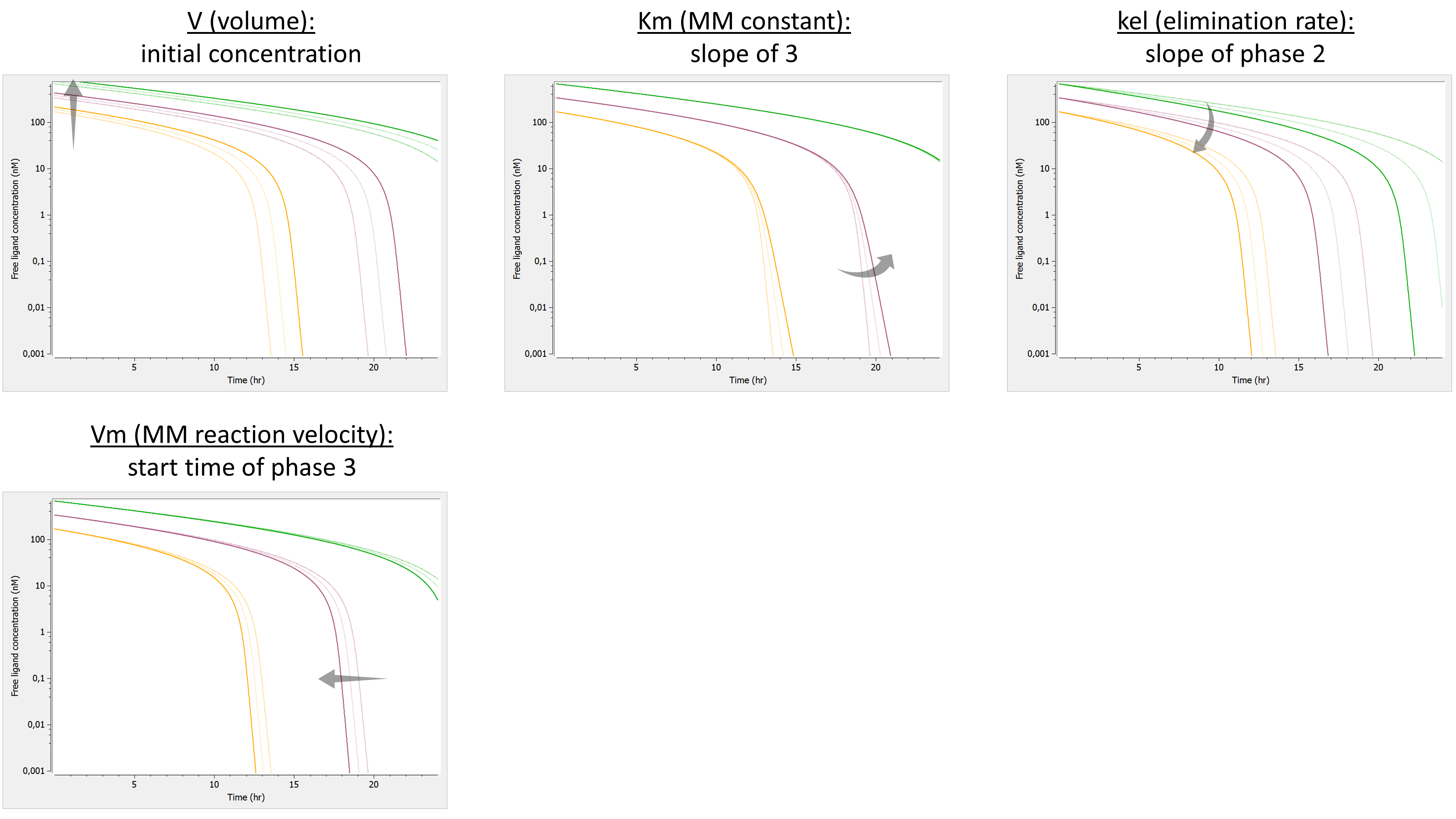
The summary picture is:

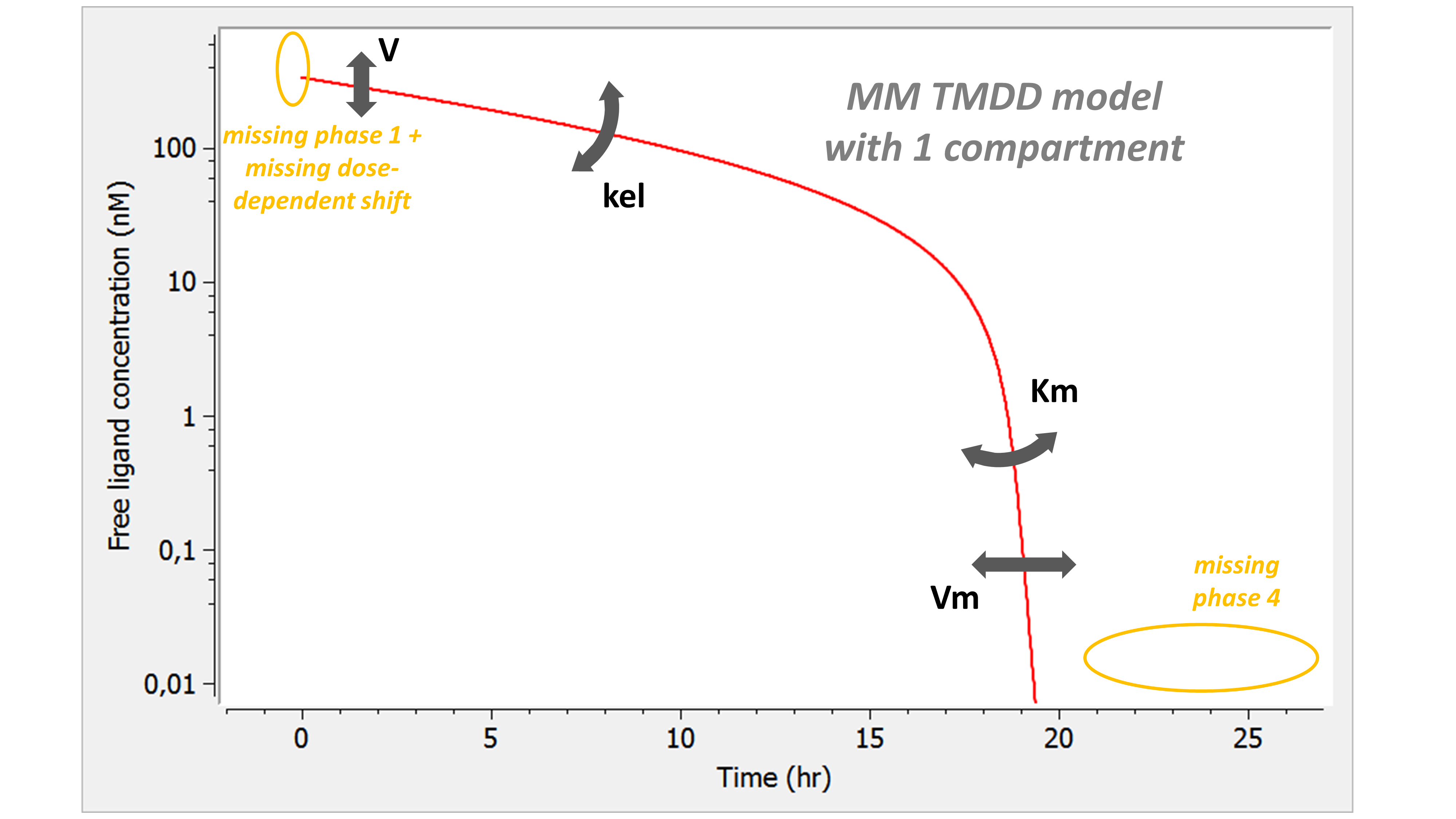
The MM model with one compartment does not capture phase 1 and phase 4. In addition, the dose-dependent shift of the initial concentration is missing: the free ligand concentration starts at the concentration obtained by dividing the dose amount by the volume, as if the ligand would not bind to the receptor. If the amount of administrated ligand is large compared to the amount of free receptor, this assumption is reasonable.

Model with 2 compartments

The MM model is often used with a second compartment. In this case the shape is modified in the following way:

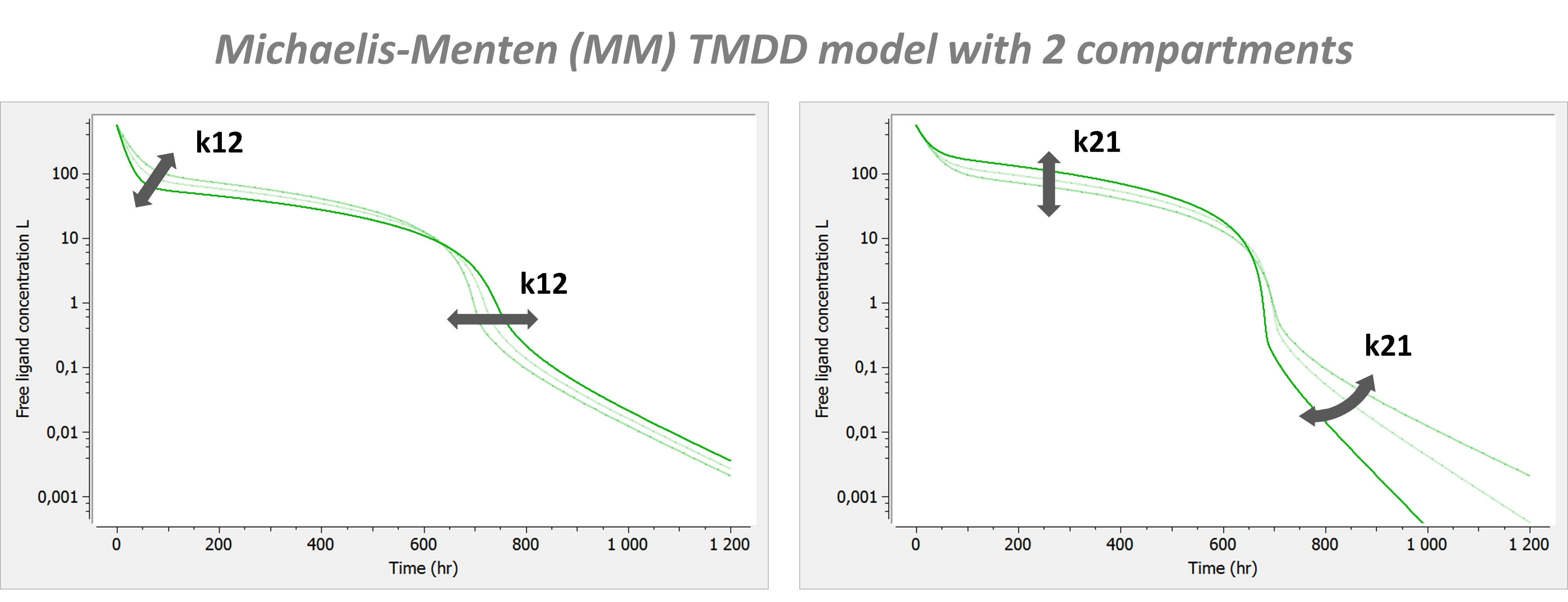
The introduction of a second compartment permits to recover a phase 4. Its flexibility is limited and linked to the effect of parameters k12 and k21 on phase 2.

Click here to go back to main TMDD page.

Detailed description of all the models