PK models with peripheral compartments

Given a central compartment defined using the compartment macro, peripheral compartments can be defined using the peripheral macro. To define rates between peripheral compartments, the transfer macro can be used.

Model with 2 peripheral compartments connected to the central compartment

This model is available in the library and can be defined using the pkmodel macro. The model can also be defined using a set of macros:

[LONGITUDINAL]
input = {V, k12, k21, k13, k31, k}

PK:
compartment(cmt=1, volume=V, concentration=Cc)
peripheral(k12, k21)
peripheral(k13, k31)
elimination(cmt=1, k)
iv(cmt=1)

OUTPUT:
output=Cc

Note that peripheral(k12, k21) implicitly defines compartment number 2 (no need to write compartment(cmt=2)). The integers i and j used in the parameter name kij (e.g 1 and 2 for k12) indicate that compartment i is connected to compartment j.

To use macro constant instead, the macro constant can be passed as input parameters, transformed into micro constant that are themselves used in the macros.

[LONGITUDINAL]
input = {V1, Cl, Q2, V2, Q3, V3}

PK:
compartment(cmt=1, volume=V1, concentration=Cc)
peripheral(k12=Q2/V1, k21=Q2/V2)
peripheral(k13=Q3/V1, k31=Q3/V3)
elimination(cmt=1, Cl)
iv(cmt=1)

OUTPUT:
output=Cc

Model for 2 peripheral compartments in a row

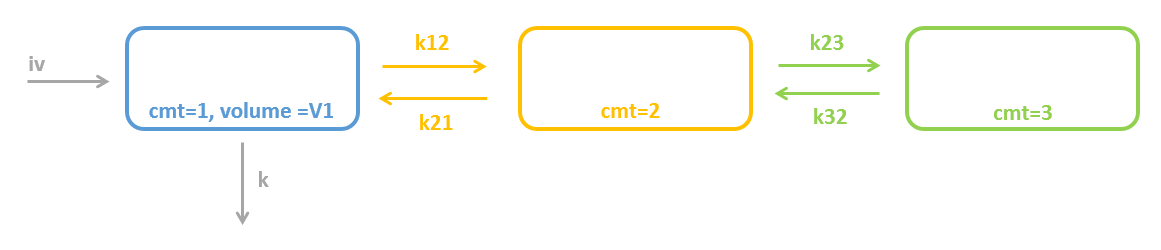
To model two peripheral compartments in a row, two peripheral macros can be used: peripheral(k12, k21) creates compartment number 2 and connects it to compartment number 1; and peripheral(k23, k32) creates compartment number 3 and connects it to compartment number 2.

[LONGITUDINAL]
input = {V, k12, k21, k23, k32, k}

PK:
compartment(cmt=1, volume=V, concentration=Cc)
peripheral(k12, k21)
peripheral(k23, k32)
elimination(cmt=1, k)
iv(cmt=1)

OUTPUT:
output=Cc

The model can also be parameterized with macro constants:

[LONGITUDINAL]
input = {V1, Cl, Q2, V2, Q3, V3}

PK:
compartment(cmt=1, volume=V1, concentration=Cc)
peripheral(k12=Q2/V1, k21=Q2/V2)
peripheral(k23=Q3/V2, k32=Q3/V3)
elimination(cmt=1, Cl)
iv(cmt=1)

OUTPUT:
output=Cc

Model with 2 interconnected peripheral compartments

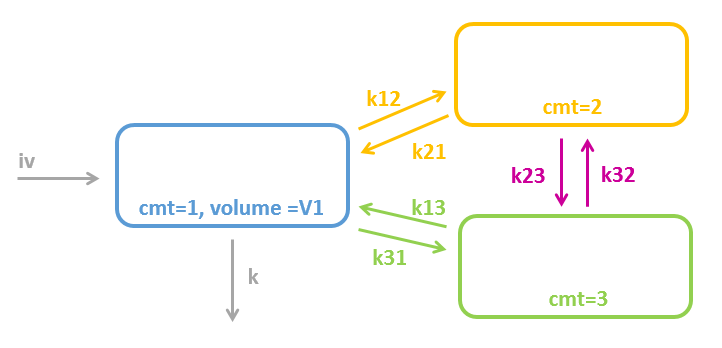
To define a model with 2 interconnected peripheral compartments, it is not possible to use only peripheral macros. Indeed, when writing:

;=== does not work ===
peripheral(k12, k21)
peripheral(k13, k31)
peripheral(k23, k32)

the third line peripheral(k23, k32) would try to create a compartment number 3, which already exists (defined by peripheral(k13, k31)). This would result into an error “conflicting compartment definition”.

Instead we can use the transfer macro:

[LONGITUDINAL]
input = {V, k12, k21, k13, k31, k23, k32, k}

PK:
compartment(cmt=1, volume=V, concentration=Cc)
peripheral(k12, k21)
peripheral(k13, k31)
transfer(from=2, to=3, kt=k23)
transfer(from=3, to=2, kt=k32)
elimination(cmt=1, k)
iv(cmt=1)

OUTPUT:
output=Cc

Model with eliminations from the central and peripheral compartments

To model a double elimination from the central and the peripheral compartments, the macro elimination can just be written twice, with the argument cmt=1 and cmt=2.

[LONGITUDINAL]
input = {V, k12, k21, k1, k2}

PK:
compartment(cmt=1, volume=V, concentration=Cc)
peripheral(k12, k21)
elimination(cmt=1, k1)
elimination(cmt=2, k2)
iv(cmt=1)

OUTPUT:
output=Cc