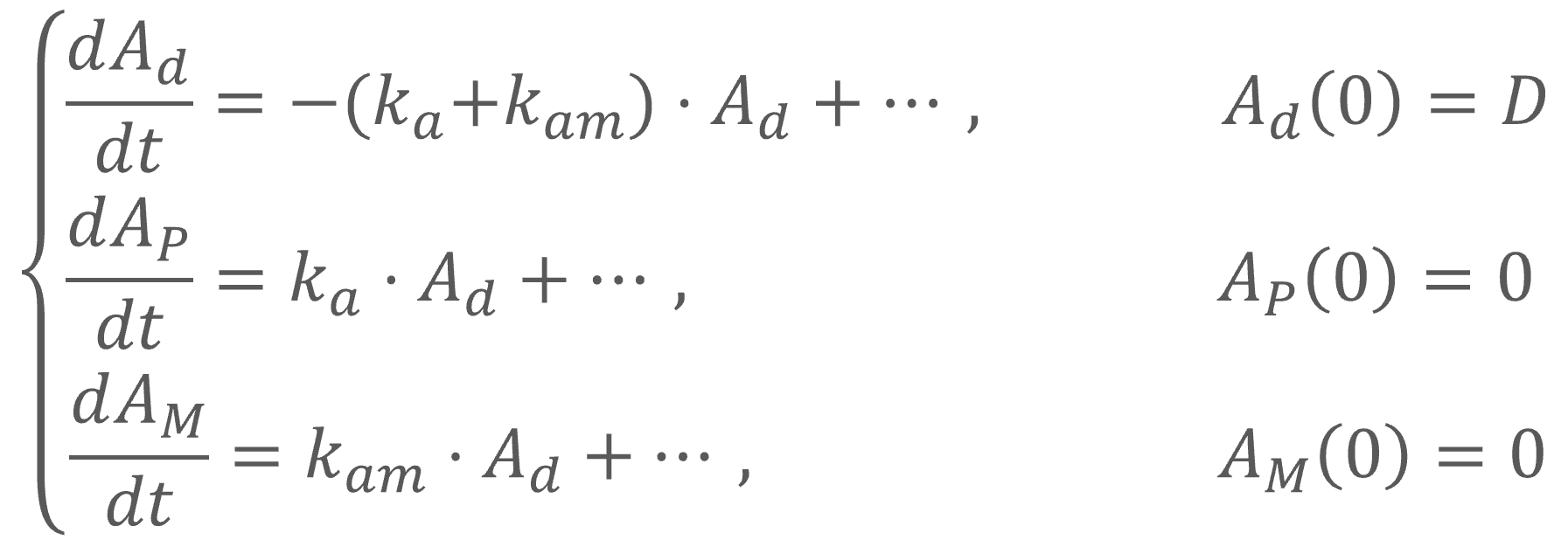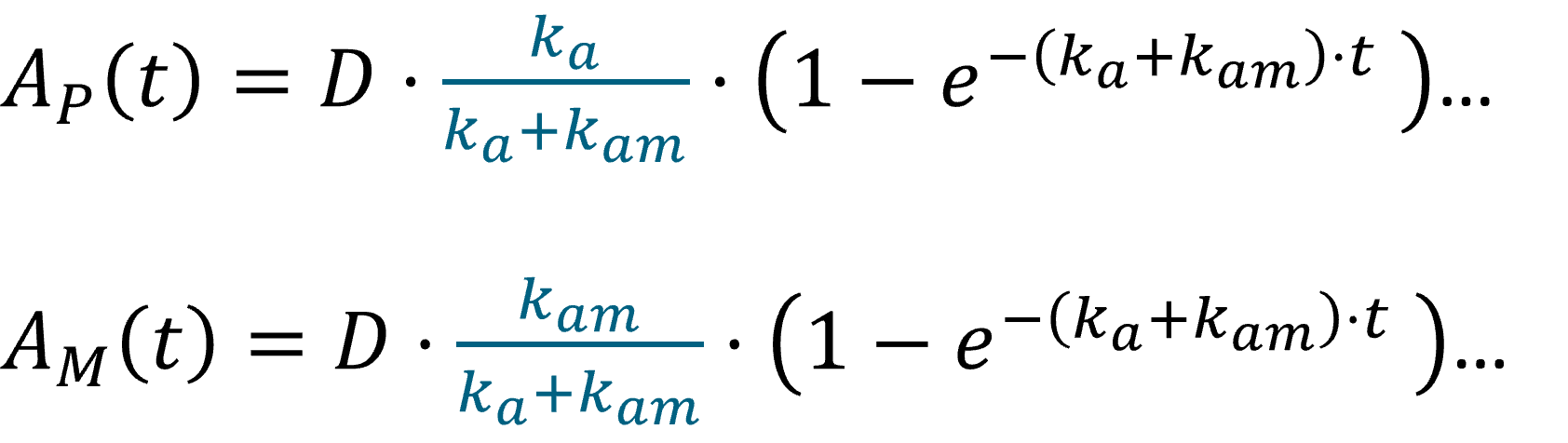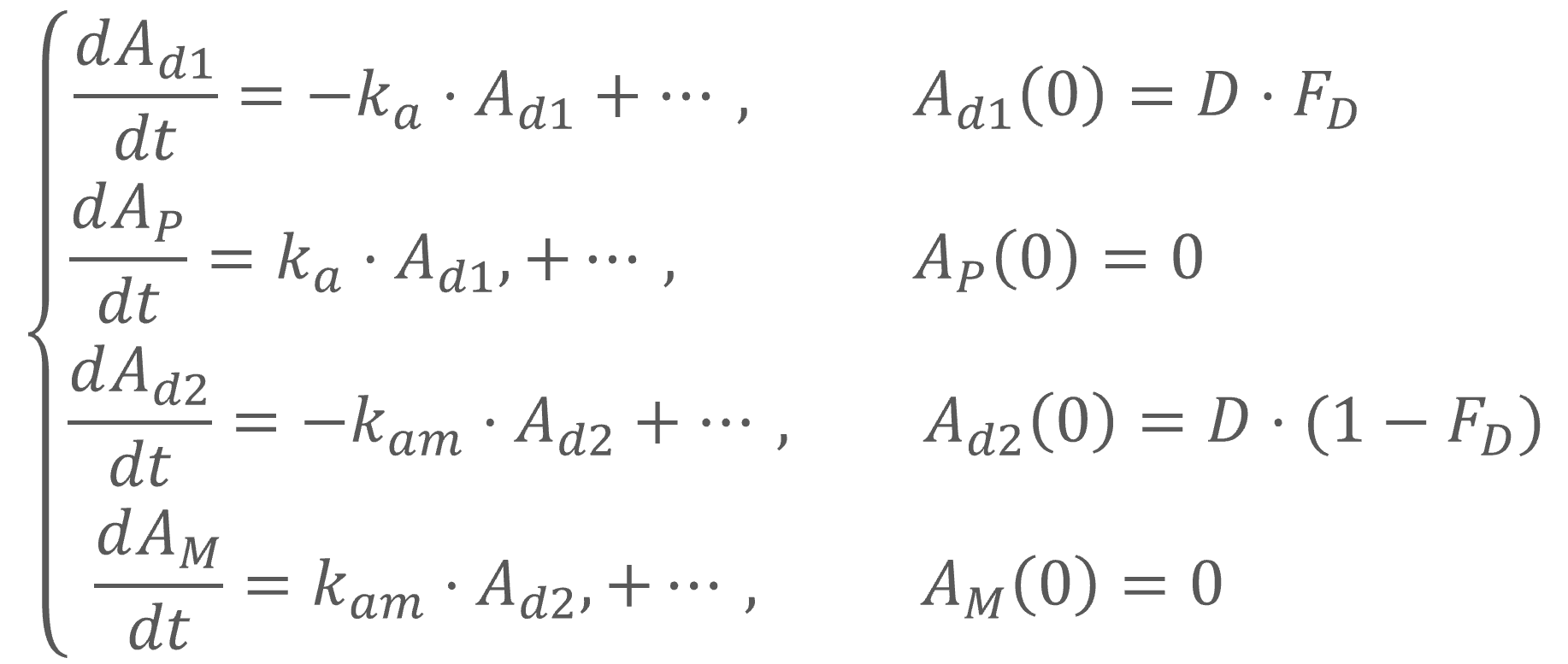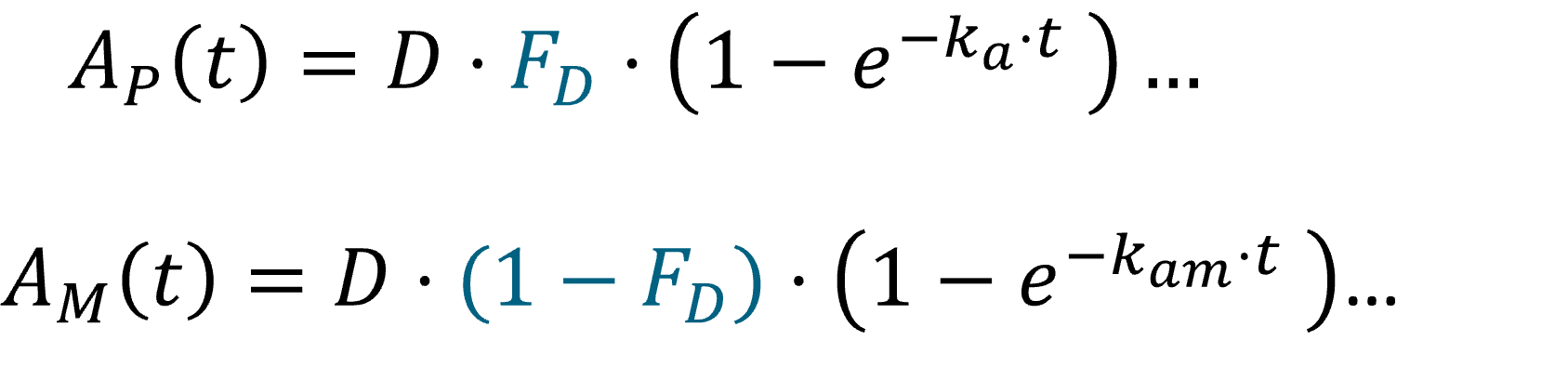Library of Parent – Metabolite models

Drugs can undergo a transformation into metabolites – pharmacologically active and/or producing adverse effects. They can impact the pharmacokinetics of the parent and drive the efficacy. But, at the same time, can rise safety concerns. Joint parent – metabolite models account for the impact of the parent-metabolite interactions on the estimation.

Library of Parent – Metabolite models includes many characteristic mechanisms, such as first pass effect, uni and bidirectional transformation and up to three compartments for parent and metabolite, which makes it an excellent tool for exploration and modeling. Implementation with mlxtran macros uses analytical solutions for faster parameter estimation and makes a great basis for the development of more complex models.

Administration

Select administration route, delay, absorption mechanism and first pass effect to correctly model drug input.

Transformation

Check non-reversible and reversible metabolic systems to predict the impact of parent-metabolite interactions.

Distribution

Explore different number of peripheral compartments independently for parent and metabolite.

Elimination

Try linear or non-linear Michaelis-Menten elimination mechanism to get a better fit.

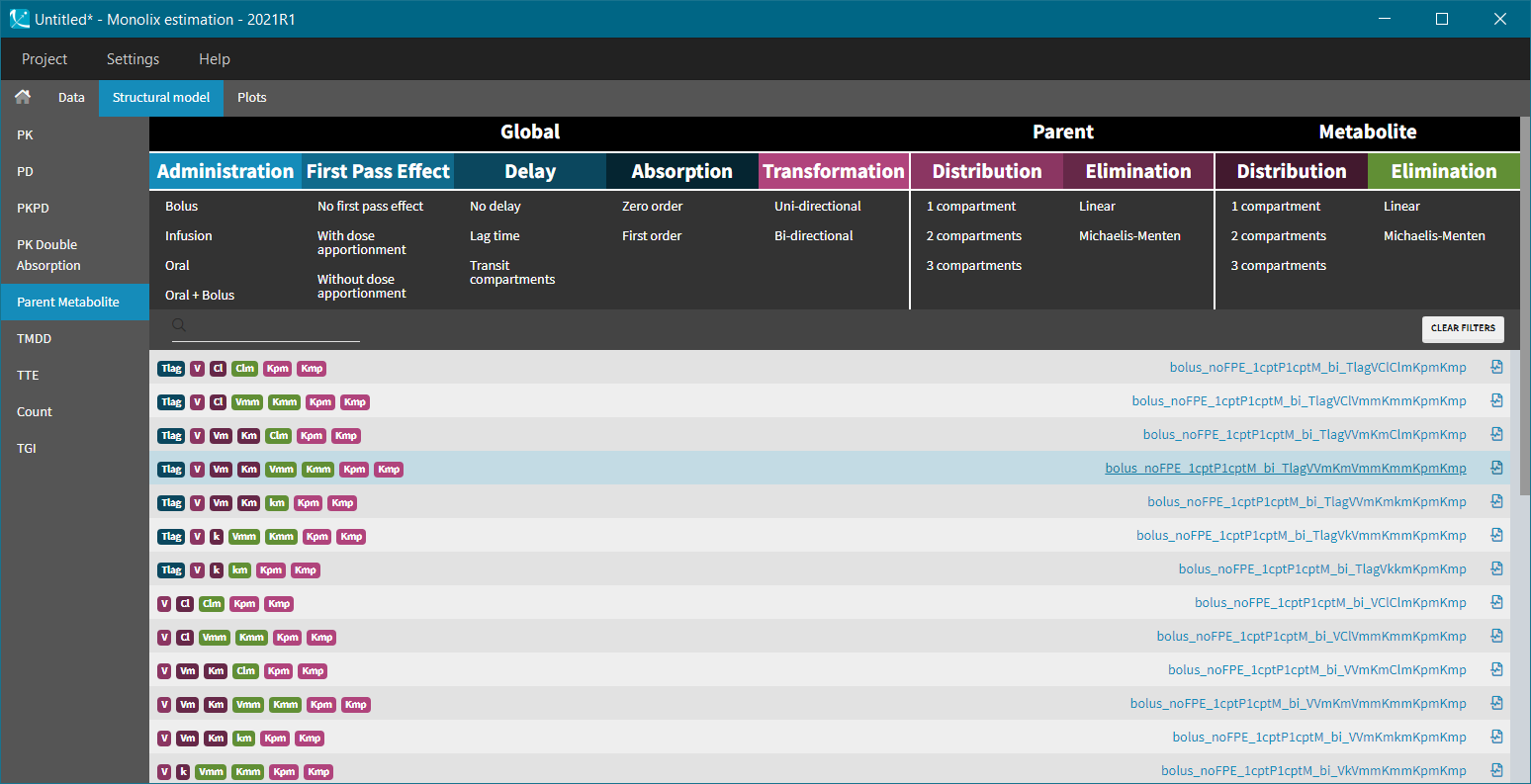
Parent-metabolite model filters

Administration

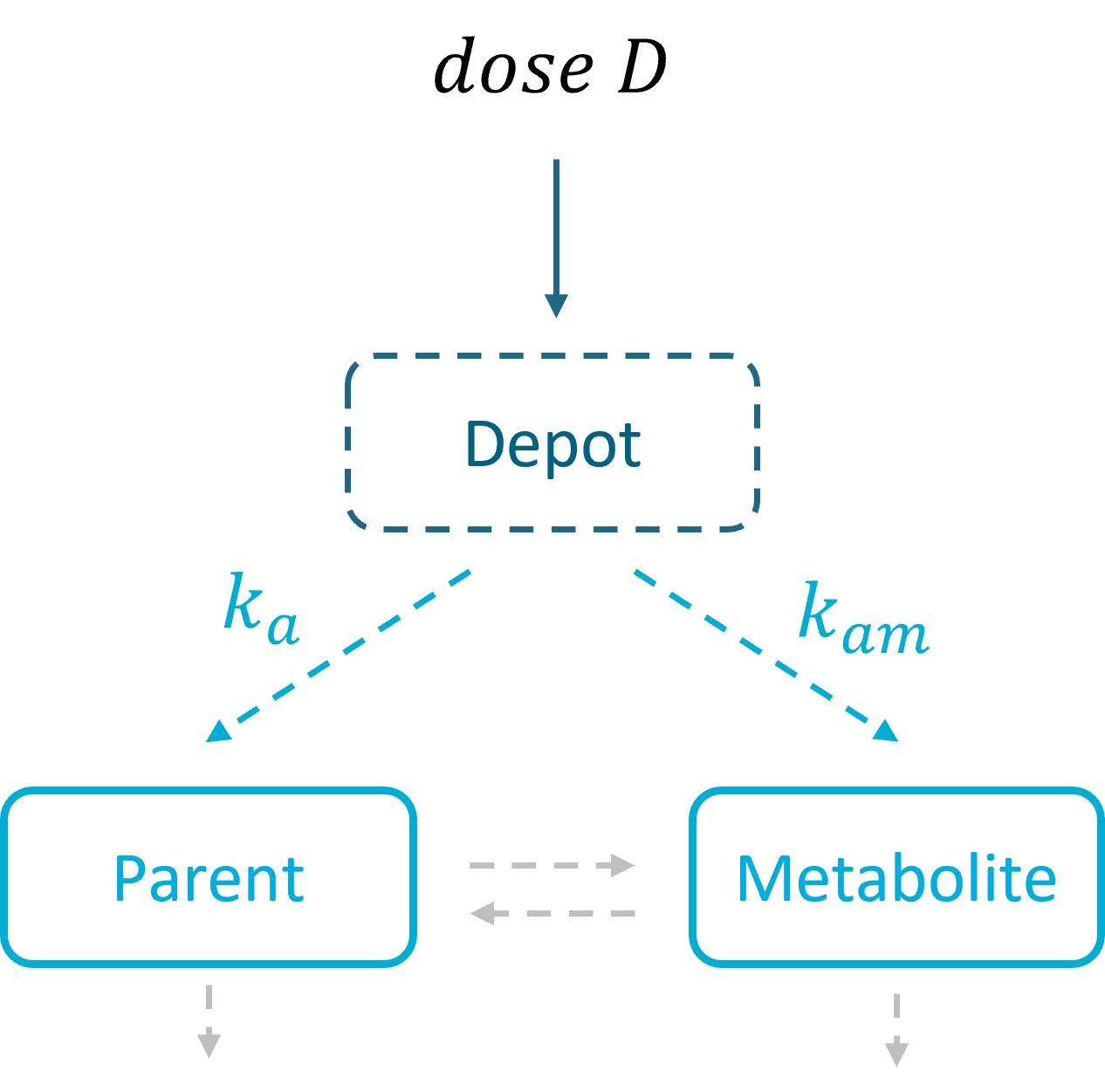
Parent-metabolite models can be combined with standard administration routes: bolus, infusion, oral/extravascular and oral with bolus. Intravenous doses are always administered to the central parent compartment. Oral doses can be in addition split between parent and metabolite – the first pass effect.

Intravenous doses (bolus, infusion) are always administered to the central parent compartment, can be with or without a time delay and does not include the first pass effect.

Oral doses can be with the following options:

with or without the first pass effect
zero (Tk0) or first order absorption process (ka for parent, kam for metabolite in case of the first pass effect)
without or with a time delay (Tlag) or with the transit compartments (Mtt, Ktr)
oral + bolus: bioavailability F (estimated as a separated parameter)

Without First Pass Effect

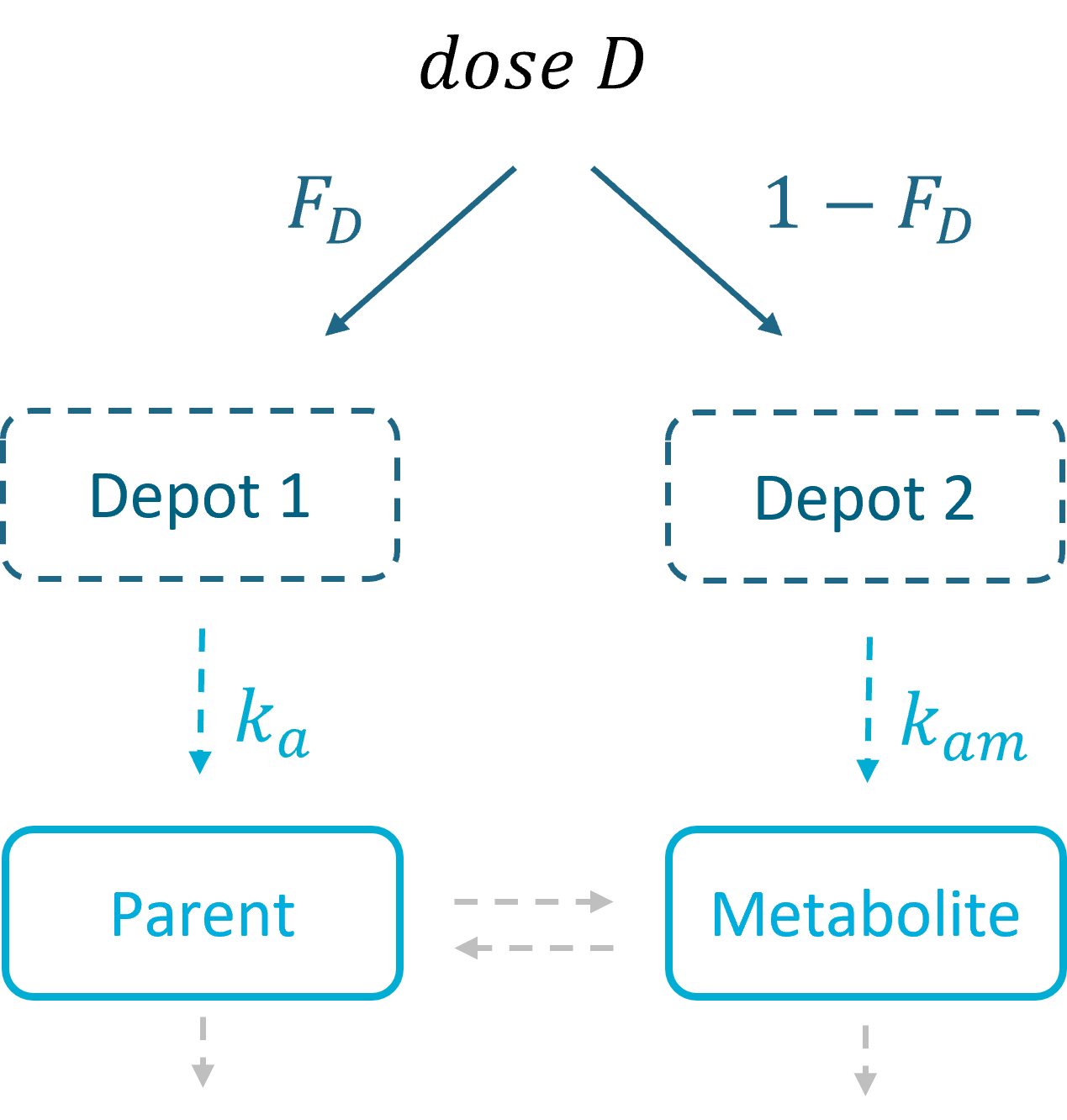
With First Pass Effect

Without dose apportionment

With dose apportionment

	Parameter
bolus, infusion	–
oral – zero order	$Tk0$
oral – first order	$ka$

Oral first order:

Oral zero order: the same formulas, with Tk0, Tk0m in place of ka, kam

Oral first order:

Oral zero order: the same formulas, with Tk0, Tk0m in place of ka, kam

First pass effect

The first pass effect is a phenomenon in which a drug undergoes any biotransformation at a specific location in the body – for example transformation of parent to metabolite before reaching its site of action or the systemic circulation. The first-pass effect can be clinically relevant when the metabolized fraction is high or when it varies significantly from individual to individual or within the same individual over time, resulting in variable or erratic absorption. It also has an impact on peak drug concentrations, which may result in parent concentration peaks occurring much earlier.

In the Monolix library, models with the first pass effect include splitting a dose – with or without dose apportionment – and absorbing one fraction in the central parent compartment (Tk0 or ka) and the other fraction in the central metabolite compartment (Tk0m or kam). The absorption process, zero or first order, is the same for parent and metabolite.

Dose apportionment means that the splitting is independent of the absorption constants (Tk0, Tk0m or ka, kam), with a fraction F_D of the dose leading to the parent and a fraction 1 – F_D leading to the metabolite prior to reach the plasma.
In models without dose apportionment, dose splitting is implicit and results from different absorption rates ka, kam (or absorption times Tk0, Tk0m).

Distribution

In the library it is possible to select different number of compartments for parent and for metabolite. The central compartments have the same volume V – identifiability issue when only parent drug is administered.

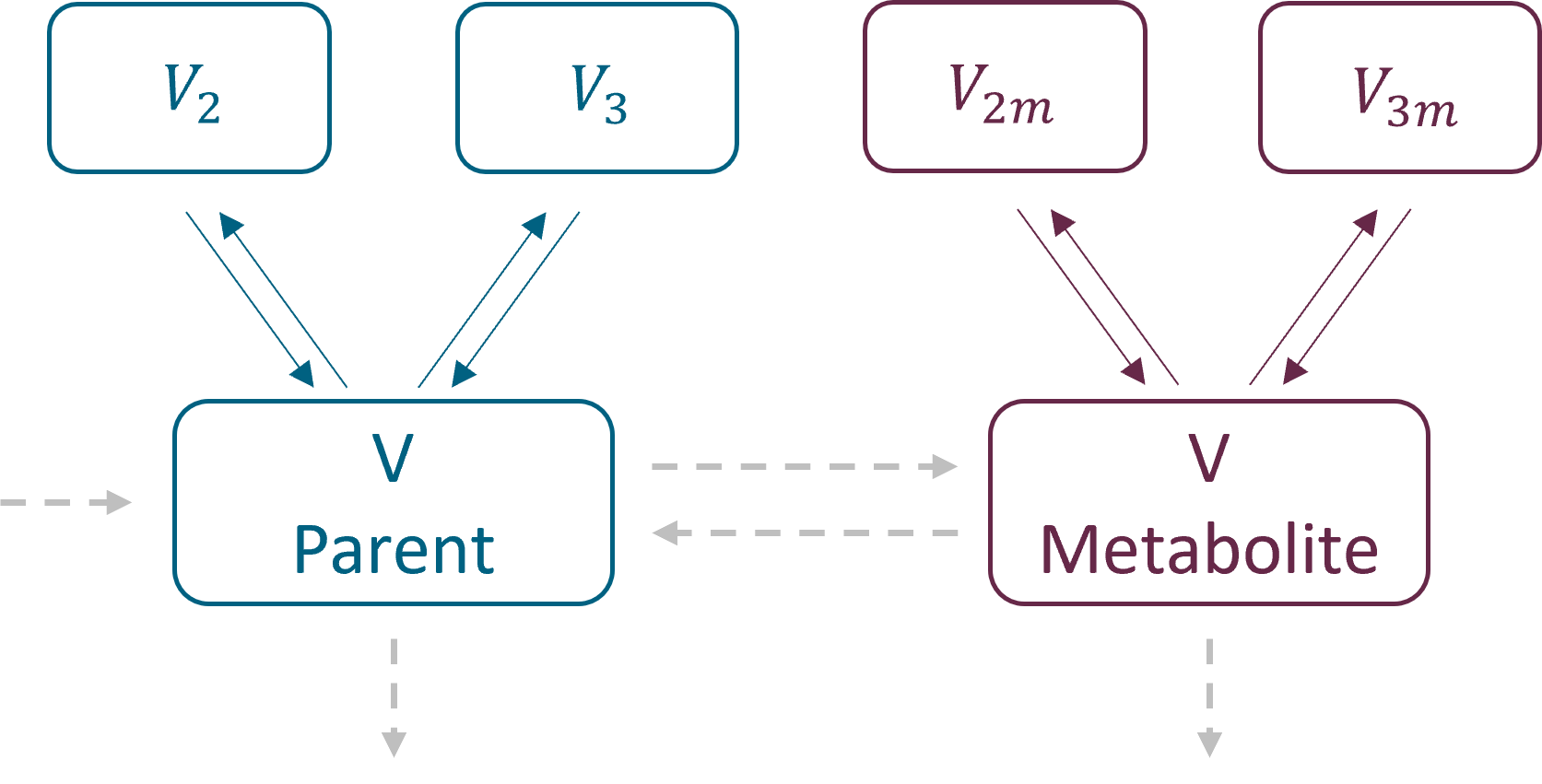
Parametrization

Parent and metabolite have the same parametrization. As for the PK and PKPD libraries, there are two parametrizations available:

with exchange rates: k12, k21 for parent and k12m, k21m for metabolite for the second compartments, and k13, k31 and k13m, k31m for the third compartments. Peripheral compartments are defined implicitly through the exchange rates, so volumes V2, V3, V2m and V3m are not estimated. The volume of central compartments is V (for both parent and metabolite)
with inter – compartment clearance: Q2, V2, Q3, V3 for parent and Q2m, V2m, Q3m, V3m for metabolite. The volume of central compartments is V1 (for both parent and metabolite), to be compatible with the PK models in case of the sequential model development.

Transformation and elimination

Drug, after administration is eliminated from the system or transformed into metabolite, which subsequently is also eliminated. In addition, metabolite can be back-transformed into a parent – it is a common process for example for amines. Both, unidirectional and reversible, transformations can be selected from the “global” section of filters in the Monolix parent-metabolite library. Elimination, linear or non-linear (Michaelis-Menten), is specific for parent and for metabolite.

Transformation:
- Kpm – transformation rate from parent to metabolite
- Kmp – transformation rate from metabolite to parent

Elimination: parent and metabolite can be eliminated with different process (linear or non-linear)
- Cl, k, Vm, Km – elimination parameters for parent
- Clm, km, Vmm, Kmm – elimination parameters for metabolite

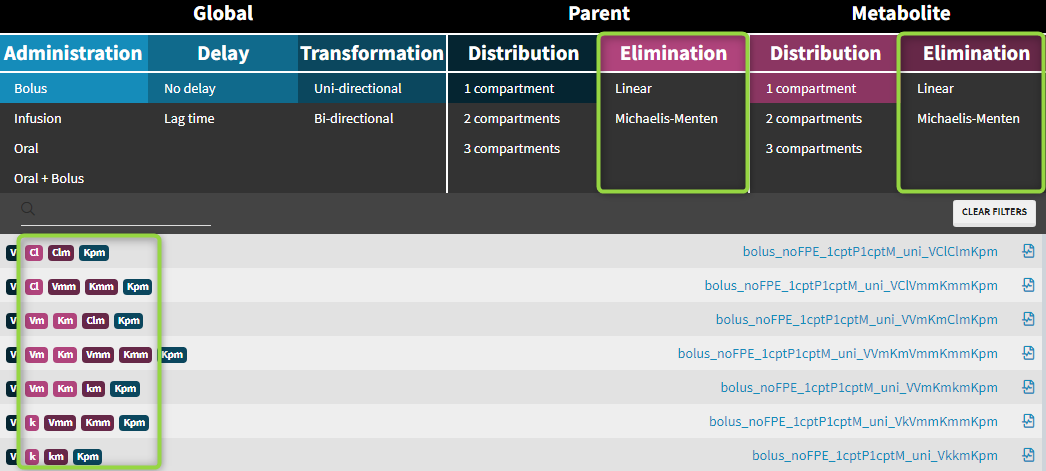
Examples:

Analytical solutions

Implementation in the Mlxtran

Example: a model with oral absorption (rate ka) of a dose D, one central compartment for parent (cmt = 1) and one for metabolite (cmt = 2), linear elimination (rates: k, km) and uni-directional transformation (rate Kpm), is the following:

$\frac{dC_{p}}{dt} = \frac{ka\cdot D}{V}\cdot e^{-ka\cdot t} - k\cdot C_{p} - K_{pm}\cdot C_{p}$
$\frac{dC_{m}}{dt} = K_{pm}\cdot C_{p} - k_{m}\cdot C_{m}$
$C_{p}(0) = 0, C_{m}(0) = 0,$
where $C_{p}, C_{m}$ are the concentrations in the central compartments of parent and metabolite respectively.

Models in the parent-metabolite Monolix library are build using mlxtran macros. For the above model:

;PK model definition for parent
compartment(cmt = 1, volume = V, concentration = Cp)
oral(cmt = 1, ka)
elimination(cmt = 1, k)

;PK model definition for metabolite
compartment(cmt = 2, volume = V, concentration = Cm)
elimination(cmt = 2, k = km)
transfer(from = 1, to = 2, kt = Kpm)

Analytical solutions

Analytical solutions, which are more accurate than numerical solutions and are faster than ODE solvers, are implemented for parent – metabolite models satisfying the following conditions:

administration (bolus, IV, oral 0 or 1st order) is to the central parent compartment only => models from the library with first pass effect (“with dose apportionment” and “without dose apportionment”) do not use analytical solutions
parameters are not time dependent (exception: dose coefficients such as Tlag, which are evaluated only once),
elimination is linear and only from the central parent and/or metabolite compartments, => models from the library with elimination = “Michaelis-Menten” do not use the analytical solutions
there are no transit compartments, => models from the library with delay = “transit compartments” do not use the analytical solution
transfer between parent and metabolite is only between their central compartments,
there are maximally two peripheral compartments for parent and maximally two for metabolite.

Comparison of the performance between analytical and numerical solutions

The following example compares the computational time (in seconds) of the parameter estimation task (SAEM) using analytical solutions (AS) and numerical solutions (ODE) for models with different number of compartments.

Dataset: simulated in Simulx N = 100 individuals, who received a single or multi oral doses. 5 or 20 measurements of both, parent and metabolite concentrations registered for each individual.
SAEM: (fixed number of iterations) 500 iterations for the exploratory phase, 200 iterations for the smoothing phase.

Times are given in seconds, and values in bold give the speed up ratio when using an analytical solution.