|
The PK/PD model library is combining our library of standard pharmacokinetic models with a library of standard pharmacodynamic models. The PK part is already described on the PK library page. Most PD models included in the PK/PD library can also be used alone (without a PK model) in the PD library, and some models from the PD library are only available alone. Here we provide general guidelines to guide you towards the standard PD model that is the most suited to your dataset. The guidelines are also summarized in this guidelines pdf.The complete list and full equations for PD models in the PD library is available in this document. Here we focus on the PD models of the PK/PD library because they are the most widely used. |
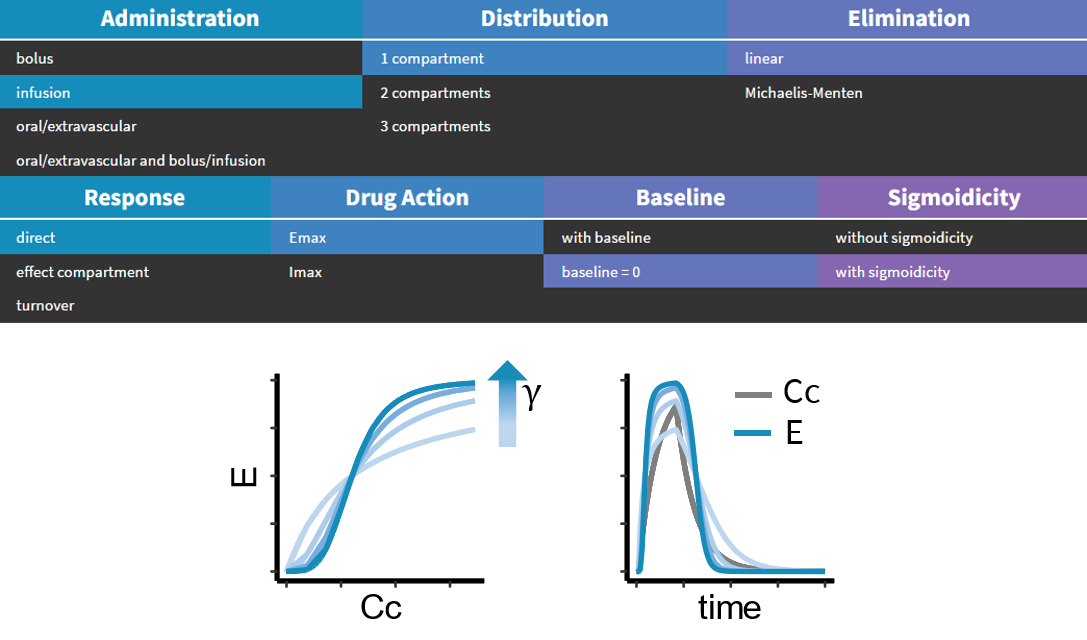
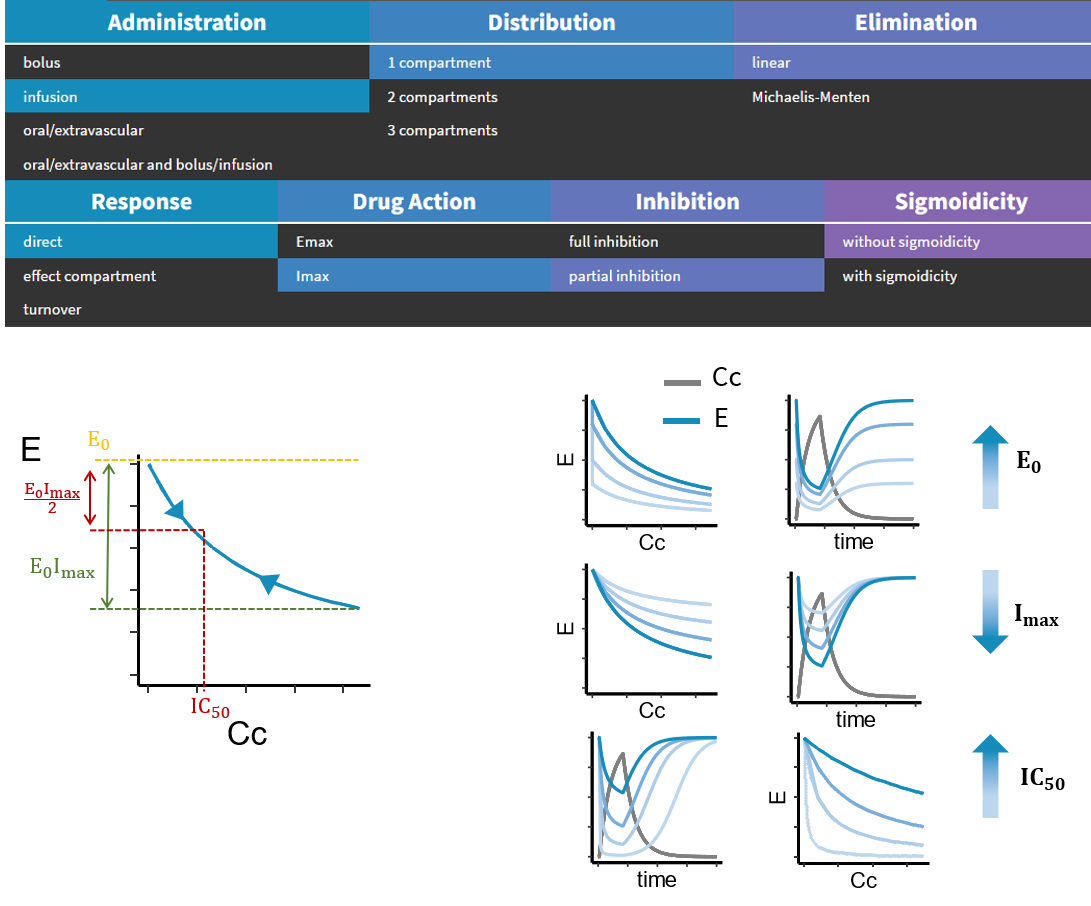
Cheat-sheet for the PD partof the PK/PD library |
PD models can be categorized by:
- the type of response linking the concentration of the drug in the central compartment \(C_C\) to the effect E or to the response R. The effect can be either direct, or with an effect compartment, or an action on a turnover rate;
- the type of drug action on the response or on the rate. It can be a stimulation or an inhibition;
- the presence or absence of sigmoidicity in this drug action.
Type of response
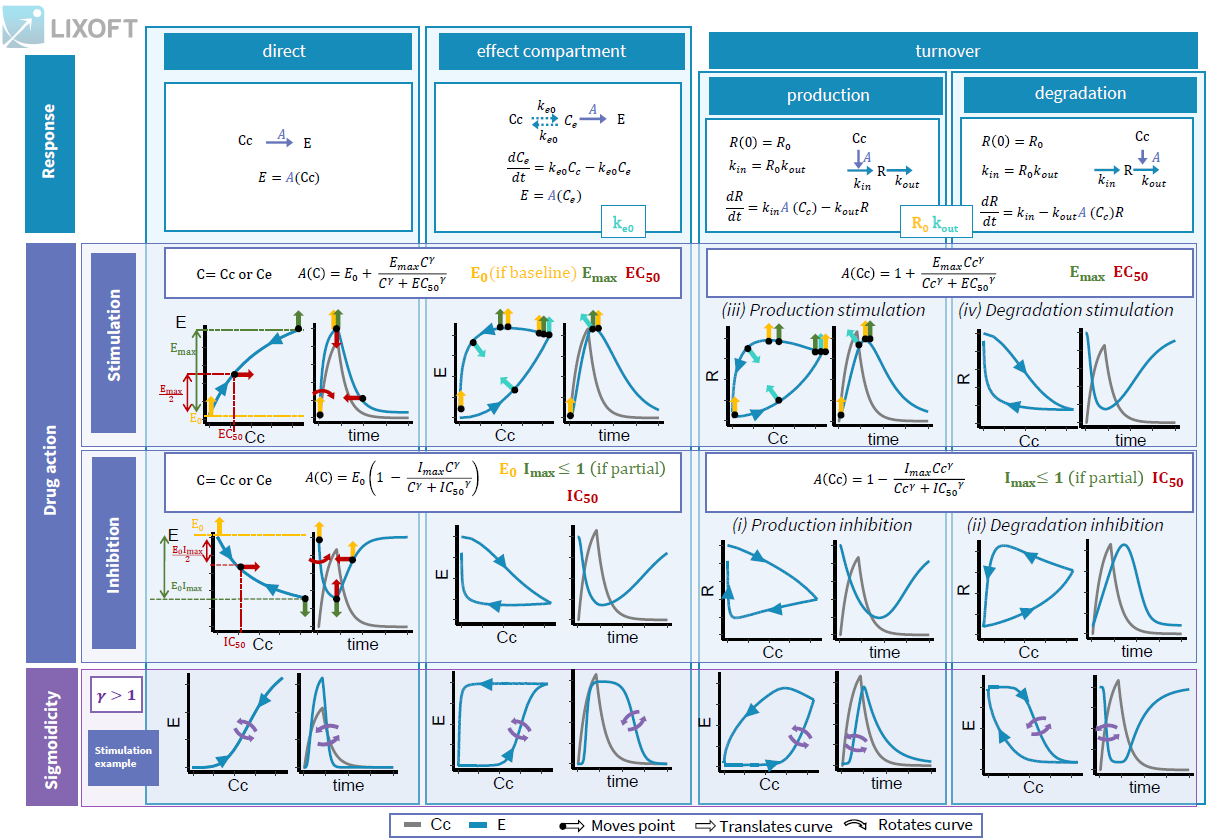
The response links the drug concentration \(C_C\) to the effect \(E\) or the response R via a function \(A\) modeling the action of the drug. The type of response specifies whether this action impacts directly the effect, or via an effect compartment or turnover rates. The content of the action function will be specified in the next section: type of drug action. To explore the differences in the types of response, we will see how they impact the PD output for a 1 compartment PK linear infusion model, with a stimulation action of the drug and without sigmoidicity.
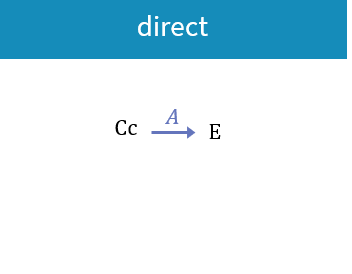
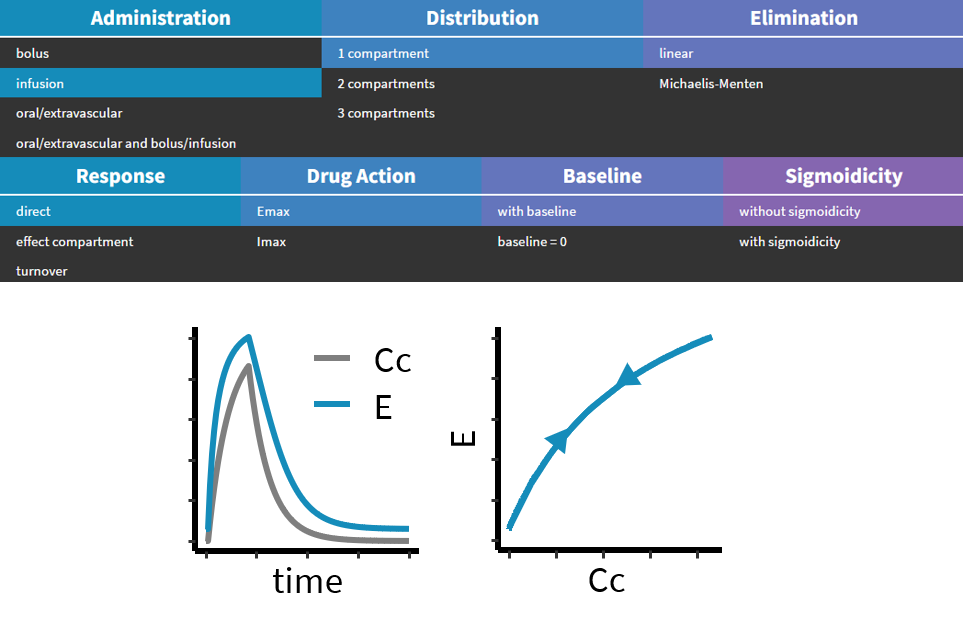
Direct
In case of a direct response, the effect \(E\) directly relates to the concentration in the central compartment \(C_C\) via
\(E = A(C_C)\)
Therefore the dynamics of the effect follow the dynamics of \(C_C\) without any delay, meaning that as soon as \(C_C\) starts decreasing, \(E\) decreases as well, and the trajectory in the phase plane \(C_C\) vs \(E\) is a single line because it follows the same route during the increase and the decrease of the signals. Below is an example simulation of a direct model with a stimulation action of the drug on the PD.
Effect compartment
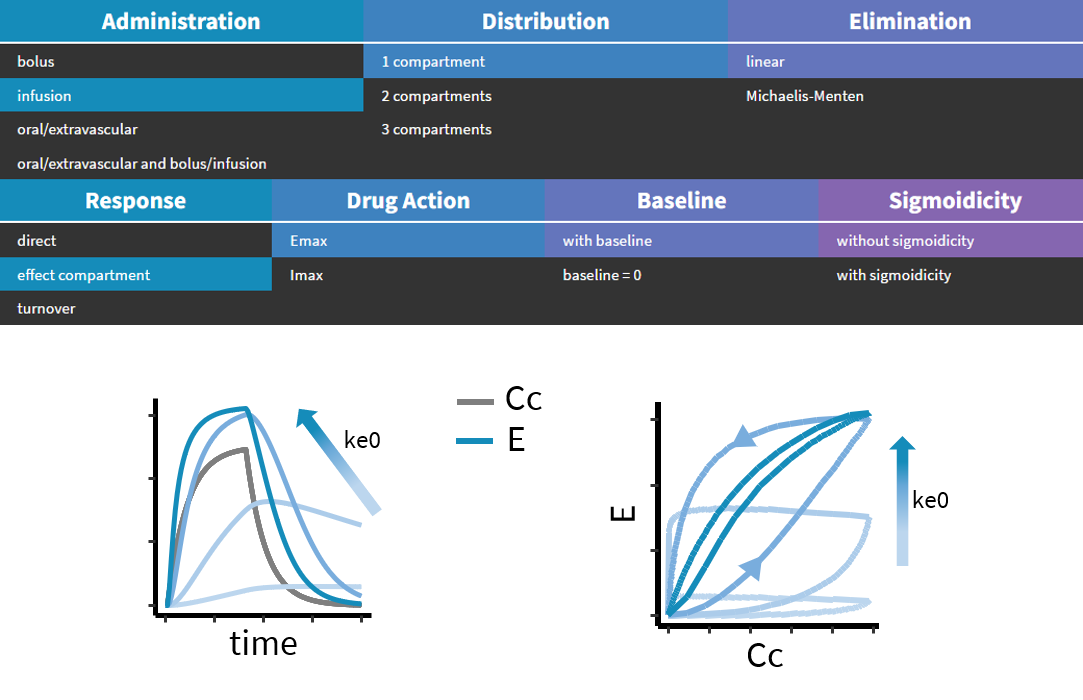
The site of action of the drug is often not be the same as the central compartment, and therefore a delay often appears between the PK and the PD measurements. To account for this delay it may be enough to add a single theoretical effect compartment with a drug concentration \(C_e\) equal to the concentration at the site of action. This theoretical compartment is assumed not to impact the concentration in the central compartment \(C_C\), therefore we write the transfer arrows between the central compartment and the effect compartment with dashed lines. A single transfer rate \(k_{e0}\) is used and the effect now directly relates to \(C_e\):
\(\frac{d C_e}{dt} = k_{e0}C_C – k_{e0}C_e\)
\(E = A(C_e)\)
Below is an example simulation of a model with an effect compartment and with a stimulation action of the drug on the PD. The higher the transfer parameter ke0, the higher the response and shorter the delay in the response.
Turnover
To model a PD response showing delay compared to the PK, it is also possible to consider that the PK concentration has an impact on the production or the degradation rate of a response variable R, as described by Sharma et al (1998). The response is then modeled with the following ODE:
- if action on the production rate: \(\frac{d R}{dt} = k_{in}A(C_C) – k_{out}R\)
- if action on the degradation rate: \(\frac{d R}{dt} = k_{in} – k_{out}A(C_C)R\)
In both cases, the model can be parameterized with the initial value of R \(R_0\) and the parameter \(k_{out}\), and \(k_{in}\) is derived as \(k_{in} = R_0 k_{out}\).
We compare below the response in the case of production stimulation and degradation inhibition. \(k_{out}\) plays a similar role as \(ke0\) in the case of an effect compartment: the higer \(k_{out}\), the shorter the delay.
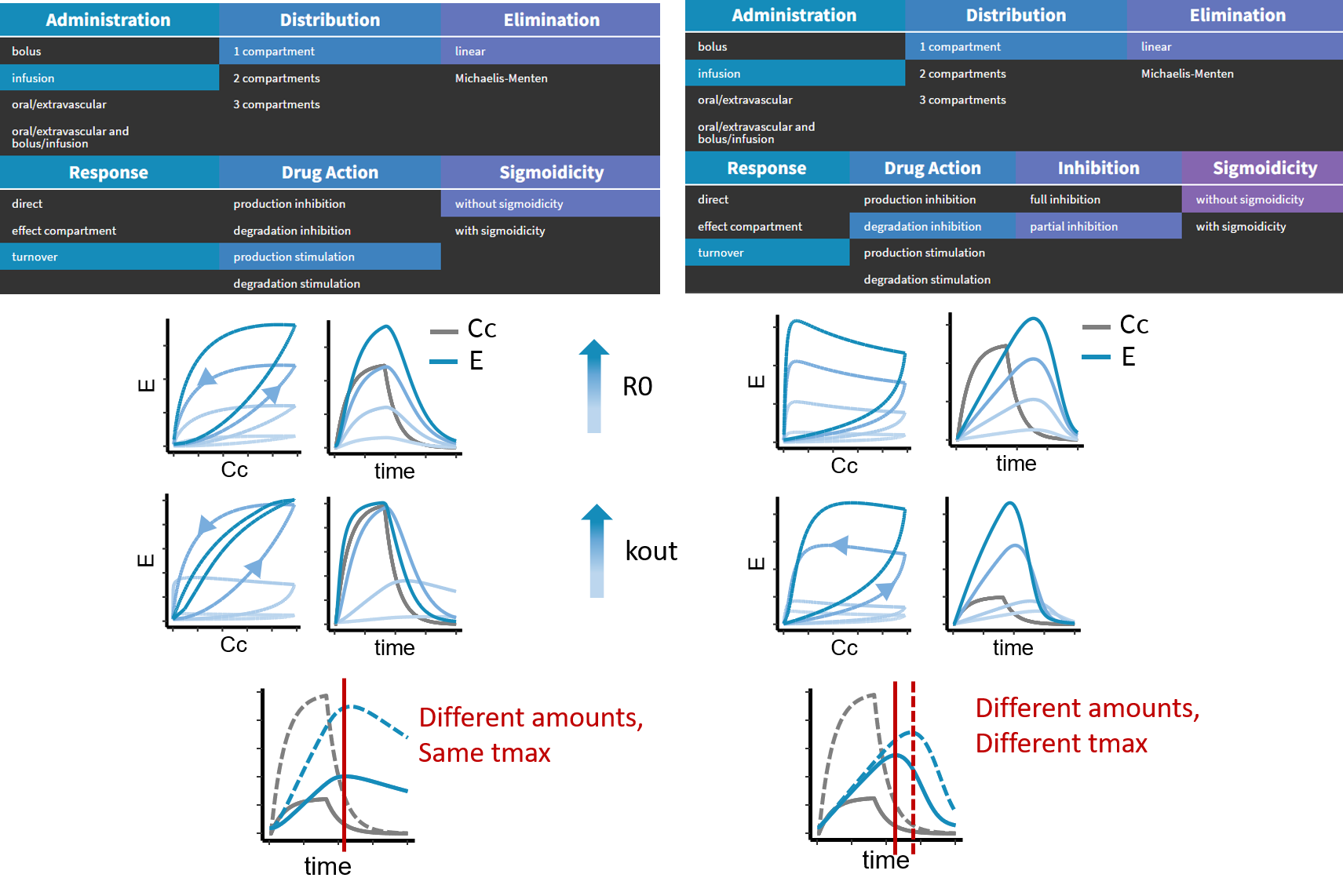
The difference between a turnover effect on the production or on the degradation is not obvious when checking the response to a single dose amount. A clear difference can be seen if two different dose amounts are given to the same individual. In the case of a turnover on production, the responses will show exactly the same delay, whereas in the case of a turnover on degradation, the delay in the response will be different for different dose amounts.
Type of drug action
The type of drug action will determine the function A relating the PK concentration to the PD effect. It can be a stimulation or an inhibition, and it is written differently depending on the type of response.
Stimulation
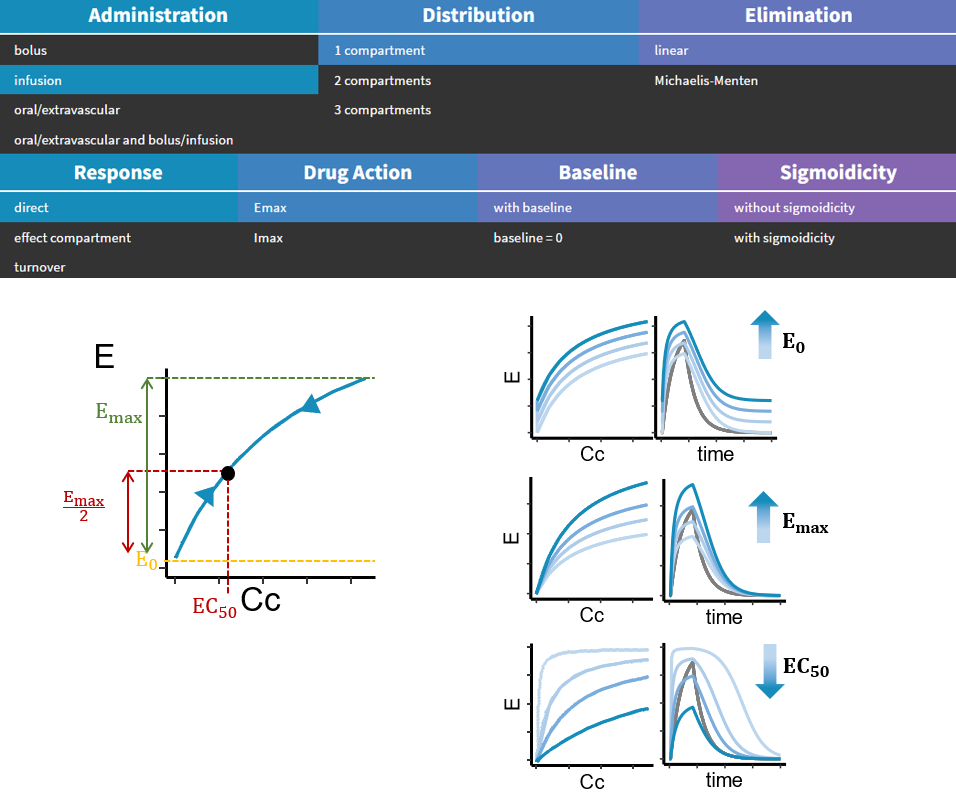
- In the case of a direct model or an effect compartment, the action of stimulation is parameterized with \(E_{max}\), \(EC_{50}\), \(\gamma\) if sigmoidicity is selected (otherwise \(\gamma = 1\)), and \(E_0\) if baseline is selected (otherwise \(E_0 = 0\)). The equation for A in the most general case is:
\(A(C) = E_0 + \frac{E_{max}C^{\gamma}}{C^{\gamma} + EC_{50}^\gamma}\)
where C is the concentration in the central compartment \(C_C\) if the model is direct, and the concentration in the effect compartment \(C_E\) if the model includes an effect compartment.
- In the case of a turnover model, the action of stimulation can happen on the production or on the degradation rate. In any case, it is parameterized with \(E_{max}\), \(EC_{50}\), and \(\gamma\) if sigmoidicity is selected, and the function always takes as an input the concentration in the central compartment \(C_C\). \(E_0\) does not appear because turnover models already include a parameter \(R_0\) to model the initial value of the response R.
\(A(C_C) = 1 + \frac{E_{max}C_C^{\gamma}}{C_C^{\gamma} + EC_{50}^\gamma}\)
Below is the example response of a direct model with a stimulation action (called Emax in the drug action section of the library) and without sigmoidicity (\(\gamma = 1\)). We show the influence of increasing E0, Emax, or the EC50. The influence of the sigmoidicity parameter \(\gamma\) is shown in the next section.
Inhibition
- In the case of a direct model or an effect compartment, the action of inhibition is parameterized with \(E_0\), \(IC_{50}\), \(I_{max}\) if partial inhibition is selected (otherwise \(I_{max} = 1\)), \(\gamma\) if sigmoidicity is selected (otherwise \(\gamma = 1\)). The equation for A in the most general case is:
\(A(C) = E_0 \Big( 1 – \frac{I_{max}C^{\gamma}}{C^{\gamma} + EC_{50}^\gamma} \Big) \)
where C is the concentration in the central compartment \(C_C\) if the model is direct, and the concentration in the effect compartment \(C_E\) if the model includes an effect compartment.
- In the case of a turnover model, the action of inhibition can happen on the production or on the degradation rate. In any case, it is parameterized with\(IC_{50}\), \(I_{max}\) if partial inhibition is selected (otherwise \(I_{max} = 1\)), and \(\gamma\) if sigmoidicity is selected, and the function always takes as an input the concentration in the central compartment \(C_C\). \(E_0\) does not appear because turnover models already include a parameter \(R_0\) to model the initial value of the response R.
\(A(C_C) = 1 – \frac{I_{max}C_C^{\gamma}}{C_C^{\gamma} + IC_{50}^\gamma}\)
Below is the example response of a direct model with an inhibition type of action (called Imax in the drug action section of the library) and without sigmoidicity (\(\gamma = 1\)). We show the influence of increasing Imax, or the IC50. The influence of the sigmoidicity parameter \(\gamma\) is shown in the next section.
Sigmoidicity
Whether it is a stimulation or an inhibition type of action, the drug action function can always involve an exponent parameter \(\gamma\). If this parameter is higher than 1, the response curve in the phase plane (\(C_C\) vs \(E\)) looks more like a sigmoid. Sigmoidicity can impact the dynamics in the PD response, making the response more switch-like due to threshold effects. If sigmoidicity is selected, the parameter \(\gamma\) will be estimated.
Below is the example response of a direct model with a stimulation type of action, and with sigmoidicity. The higher the gamma, the steeper the dose response, and the more square-like the time response.