In some cases, for instance in case of transporter-mediated uptake, the absorption from the depot compartment into the central compartment can saturate. To model this phenomenon, one can replace the first-order rate of absorption by a Michaelis-Menten term.
Examples of drugs displaying a saturating absorption include Phenylbutazone, Naproxen, Chlorothiazide, beta-lactam antibiotics and are reviewed in:
Mlxtran model
To describe a saturable absorption, the depot compartment must be explicitly described and the model must be written as an ODE system. Below we present a one-compartment model with linear elimination and saturable absorption.
The depot macro permits to add the doses defined in the data set to the amount in the depot compartment. The Michaelis-Menten term is written using the amount of the depot compartment instead of the concentration as the volume needed to calculate the concentration is unidentifiable.
[LONGITUDINAL]
input={Vm, Km, V, Cl}
PK:
depot(target=Ad)
EQUATION:
t_0 = 0
Ad_0 = 0
Ac_0 = 0
ddt_Ad = -Vm*Ad/(Ad+Km)
ddt_Ac = Vm*Ad/(Ad+Km) - Cl/V*Ac
Cc = Ac/V
OUTPUT:
output = {Cc}
Exploration with Mlxplore
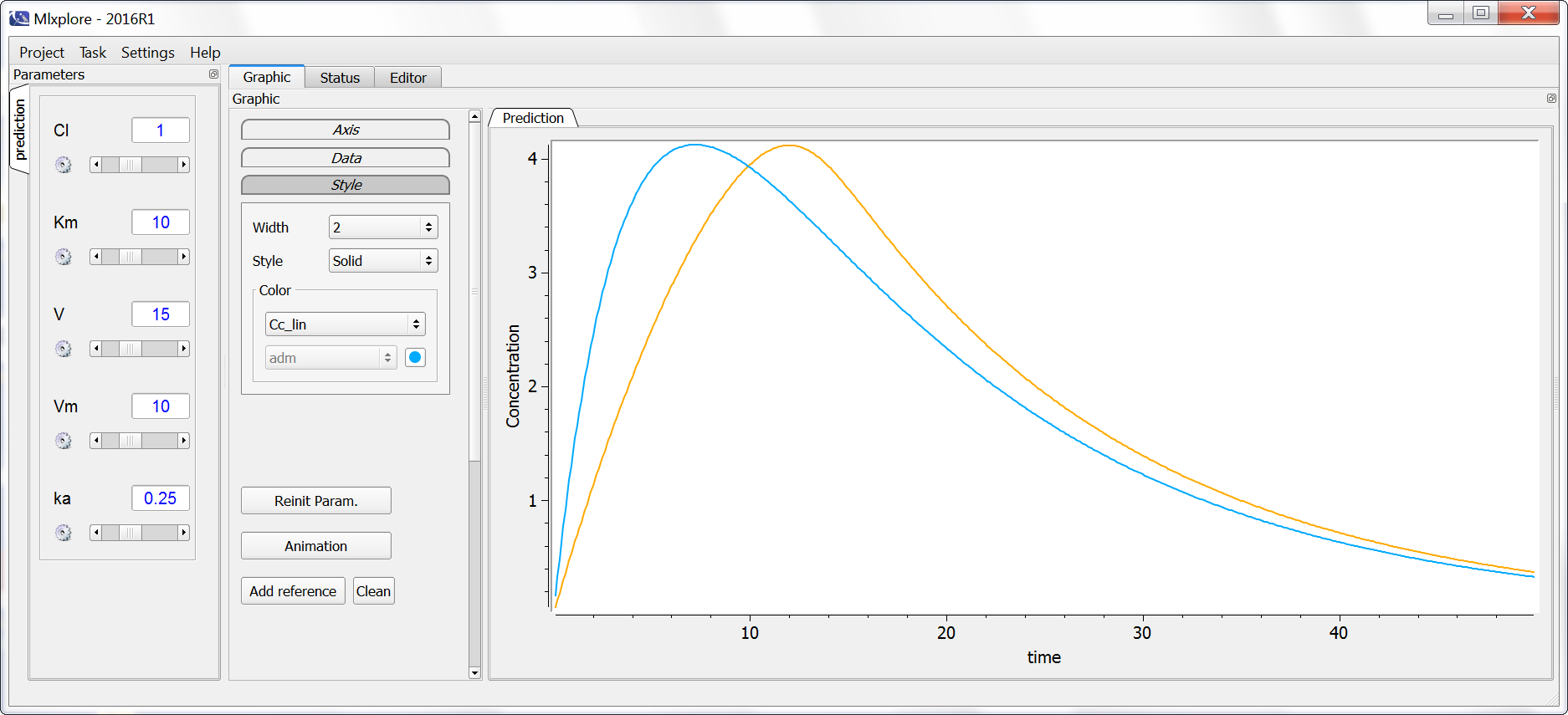
We explore the difference between a linear and a saturating absorption using the following Mlxplore script:
<MODEL>
[LONGITUDINAL]
input={Vm,Km,ka,V,Cl}
PK:
; depot for saturating absorption
depot(target=Ad)
; model for linear absorption
Cc_lin = pkmodel(ka,V,Cl)
EQUATION:
; model for saturating absorption
t_0 = 0
Ad_0 = 0
Ac_0 = 0
ddt_Ad = -Vm*Ad/(Ad+Km)
ddt_Ac = Vm*Ad/(Ad+Km) - Cl/V*Ac
Cc_sat = Ac/V
<PARAMETER>
Vm = 10
Km = 10
V = 15
Cl = 1
ka = 0.25
<DESIGN>
[ADMINISTRATION]
adm = {time=0, amount=100}
<OUTPUT>
list={Cc_sat, Cc_lin}
grid=0.1:0.1:50
<RESULTS>
[GRAPHICS]
p1 = {y={Cc_sat,Cc_lin}, ylabel='Concentration', xlabel='time'}
Below the linear absorption is shown in blue and the saturating in orange: