Purpose
The macro absorption/oral enables to link the administration and the model, for zero-order and first-order absorption processes (for bolus administrations, use the iv macro instead). For Mlxtran the macro names ‘absorption’ and ‘oral’ can be used interchangeably. The administration can either be defined in a data set when Monolix is used, or the administration can be defined via an administration design definition when Mlxplore or Simulx are used. In order to handle models with several administrations each administration has a unique identifier called adm. This identifier must be defined in the data set or in the administration design definition, and used in the absorption/oral macro.
Arguments
The absorption/oral macro can be used for zero-order and first-order absorptions. The arguments common to the two absorptions are:
- adm: Administration type of doses subject to the absorption process. Its default value is 1. Alias: type. Thus, when defining a treatment in Mlxplore for example, instead of defining a target, the user should define an administration type and apply the dedicated absorption process on it.
- Tlag: Lag time before the absorption. Its default value is 0.
- p: Final proportion of the absorbed amount. It can affect the effective rate of the absorption, not its duration. p can take any positive value (including > 1). Its default value is 1.
- cmt: Label of the compartment called in by the absorption process. Its default value is 1.
To define a zero-order or first-order absorption, the additional arguments defined below are needed.
Arguments specific to a zero-order absorption (i.e infusion)
To define a zero-order absorption, the following argument must be added:
- Tk0: Duration of the zero order absorption. Mandatory to define a zero-order absorption.
Example:
; zero order absorption process for the doses of type 1, in compartment 1 with a delay Tlag of 1 and a duration Tk0 absorption(adm=1, cmt=1, Tlag=1, Tk0 = 2, p=1)
Arguments specific to a first-order absorption
To define a first-order absorption, the following arguments can be added:
- ka: Rate of the first order absorption. Mandatory to define a first-order absorption.
- Ktr: Transit rate.
- Mtt: Mean transit time for the absorption.
Example:
PK: ; first order absorption process for the doses of type 1, in compartment 1 with a delay Tlag of 1 and a rate ka absorption(type=1, cmt=1, Tlag=1, ka)
Note: in case of transit compartments, the mean transit time is defined as Mtt = (n+1)/Ktr with n the number of transit compartments (excluding the depot compartment and the absorption compartment):
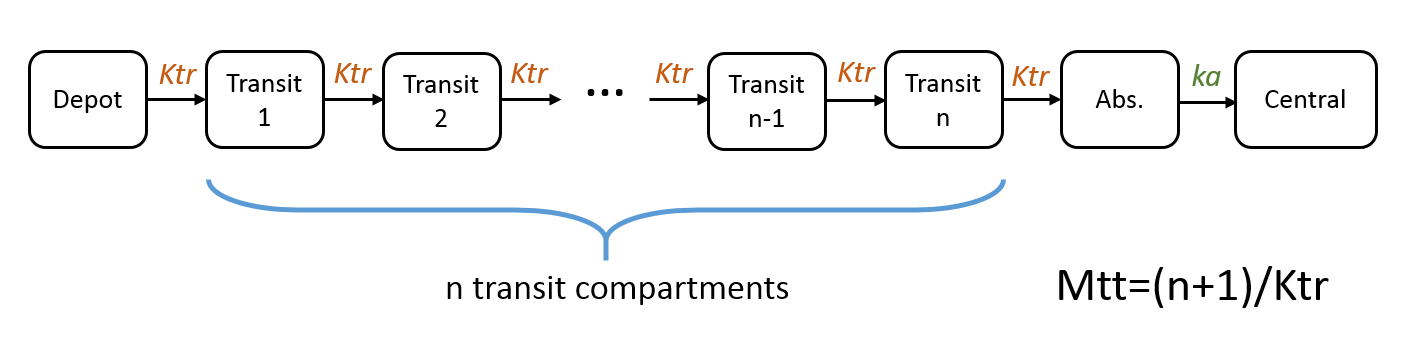
The implementation is the same as described in Savic et al, “Implementation of a transit compartment model for describing drug absorption in pharmacokinetic studies” (2007), except that to approximate the factorial n!, we use the gamma function, which is more precise, instead of the Stirling formula.
In case of multiple doses, we assume that the previous dose has been completely absorbed (i.e concentration is the Abs compartment is almost zero) when the next dose is administered. If this is not the case, the remaining concentration in the Abs compartment is erased when the next dose is applied, leading to a loss of dose amount entering the system.
Example with mixed absorptions
Some drugs can exhibit atypical absorption profiles with for instance a zero-order absorption followed by a first-order absorption, or first and zero-order simultaneously.
Sequential absorption, zero-order followed by first-order
In the example below, a fraction F1 of the drug is absorbed via a zero-order process for a duration Tk0. The remaining fraction 1-F1 is then absorbed via a first-order process, which starts with a lag-time Tk0 (i.e at the end of the zero-order absorption phase).
PK: absorption(adm=1, cmt=1, Tk0, p=F1) absorption(adm=1, cmt=1, ka, p=1-F1, Tlag=Tk0)
Simultaneous first-order and zero-order absorption
In the example below, a fraction F1 of the drug is absorbed via a first-order process (with absorption rate ka). Simultaneously the remaining fraction 1-F1 is absorbed via a zero-order process.
PK: absorption(adm=1, cmt=1, ka, p=F1) absorption(adm=1, cmt=1, Tk0, p=1-F1)
A lag time for one or the other process can be added if necessary.
Example with Mlxplore: Comparison of absorptions
In the presented example, we show the difference between the two absorption processes. In addition, the effect of the Ktr and Mtt parameters is explored in a third model. The model is implemented in the following file mlxplore_Absorption.txt.
<MODEL>
[LONGITUDINAL]
input = {V, Tlag, ka, Tk0, Ktr, Mtt}
PK:
compartment(cmt=1, amount=A1, concentration=Cc_zoa, volume=V)
absorption(cmt=1, adm=1, Tk0)
elimination(cmt=1, k=1)
compartment(cmt=2, amount=A2, concentration=Cc_foa, volume=V)
absorption(cmt=2, adm=1, Tlag, ka)
elimination(cmt=2, k=1)
compartment(cmt=3, amount=A3, concentration=Cc_foaT, volume=V)
absorption(cmt=3, adm=1, Tlag, ka, Ktr, Mtt)
elimination(cmt=3, k=1)
EQUATION:
ddt_A1 = 0
ddt_A2 = 0
ddt_A3 = 0
<DESIGN>
[ADMINISTRATION]
adm = {time=5, amount=1, adm=1}
<PARAMETER>
V = 10
Tlag = 2
ka = .5
Tk0 = 2
Ktr = 3
Mtt = 2
<OUTPUT>
grid = 0:.05:20
list = {Cc_zoa, Cc_foa, Cc_foaT}
<RESULTS>
[GRAPHICS]
p = {y={Cc_zoa, Cc_foa, Cc_foaT}, ylabel='Concentrations', xlabel='Time'}
The three concentrations are presented in the following figure.
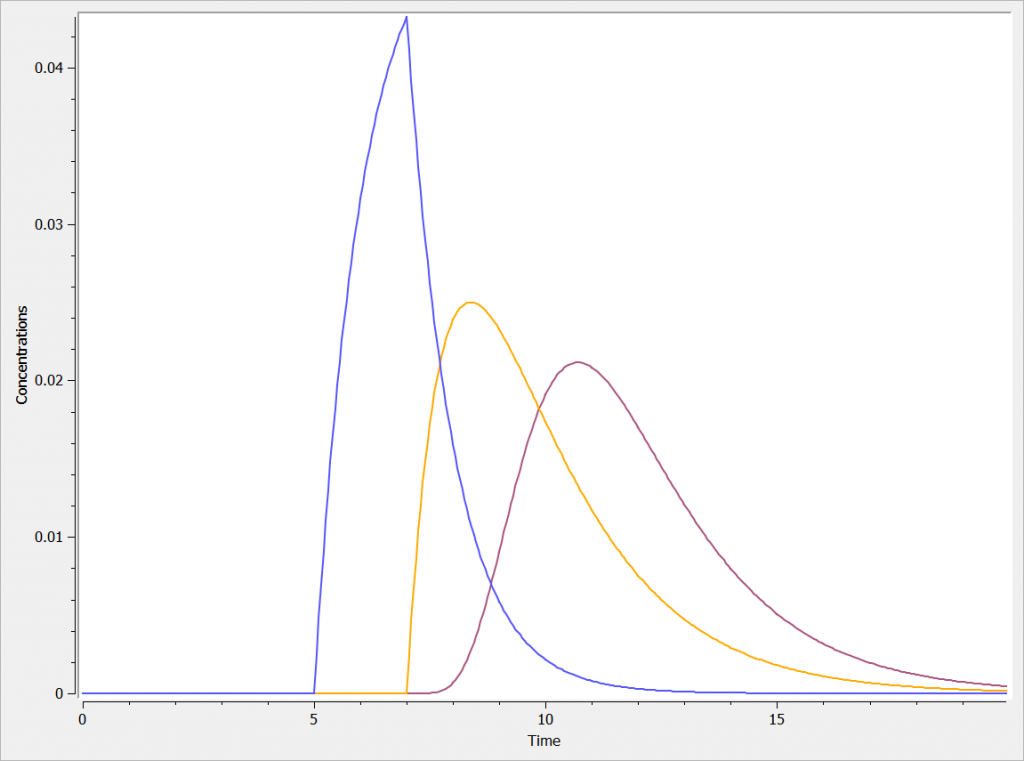
One can clearly see the differences between the zero order absorption (Cc_zoa in blue), the first order absorption (Cc_foa in orange) and the absorption with transit compartments (in purple).
Rules and Best Practices:
- We encourage the user to use all the fields in the macro to guarantee no confusion between parameters
- Format restriction (non compliance will raise an exception)
- The value after cmt= and type= are necessarily integers.
- The value after Tlag=, p=, V=, ka=, Tk0=, Ktr=, Mtt= can be either a double or replace by an input parameter. Calculations are not supported.
- The associated treatment or administration can not be defined with a rate nor an infusion timing (RATE and TINF column-types in the data set). If a rate or an infusion timing is present, the user can use the iv macro and/or define a compartment to define the dynamics of the absorption.