Irreversible binding + constant Rtot TMDD model

We here present the system of equation corresponding to the constant Rtot + irreversible binding TMDD model, as well as the model behavior.

Equations

In the same way as the rapid binding + constant Rtot assumptions lead to the Wagner model, we can combine the irreversible binding and constant Rtot approximations to obtain a new model. To our knowledge, this approximation has not yet been presented in the literature. The equations read:

\begin{array}{ccl} \dfrac{dL}{dt} &=& \dfrac{\textrm{In}(t)}{V} - k_{\textrm{el}}L-k_{\textrm{on}}\:L(R_0 -P) \\ \dfrac{dP}{dt} &=& k_{\textrm{on}}\:R_0\:L - (k_{\textrm{int}} + k_{\textrm{on}}L)\:P \end{array}

with L the concentration of the ligand in plasma and P the concentration of the complex. V is the volume of the central compartment for the ligand, kel the linear elimination rate for the ligand, kon the binding rate, R0 the initial receptor concentration, and kint the degradation rate of the complex. In(t) represents the input function, corresponding to the input rate (amount per unit time) of the ligand into the central compartment due to the ligand administration.

With two compartments, we obtain:

\begin{array}{ccl} \dfrac{dL}{dt} &=& \dfrac{\textrm{In}(t)}{V} - k_{\textrm{el}}L-k_{\textrm{on}}\:L(R_0 -P) - k_{\textrm{12}}\:L + k_{\textrm{21}}\:A/V \\ \dfrac{dP}{dt} &=& k_{\textrm{on}}\:R_0\:L - (k_{\textrm{int}} + k_{\textrm{on}}L)\:P \\ \dfrac{dA}{dt} &=& k_{\textrm{12}}\:L\:V - k_{\textrm{21}}\:A \end{array}

with A the amount of ligand in peripheral tissues, k12 the rate of transfert from central to peripheral, and k21 the rate in the opposite direction.

The system has 5 parameters: same number of parameters as in the Wagner model, and one less compared to QE/QSS, irreversible binding and constant Rtot.

Model properties

We investigate the influence of each parameter on the typical free ligand concentration-time shape for several dose amounts (bolus administration).

Here is the summary picture:

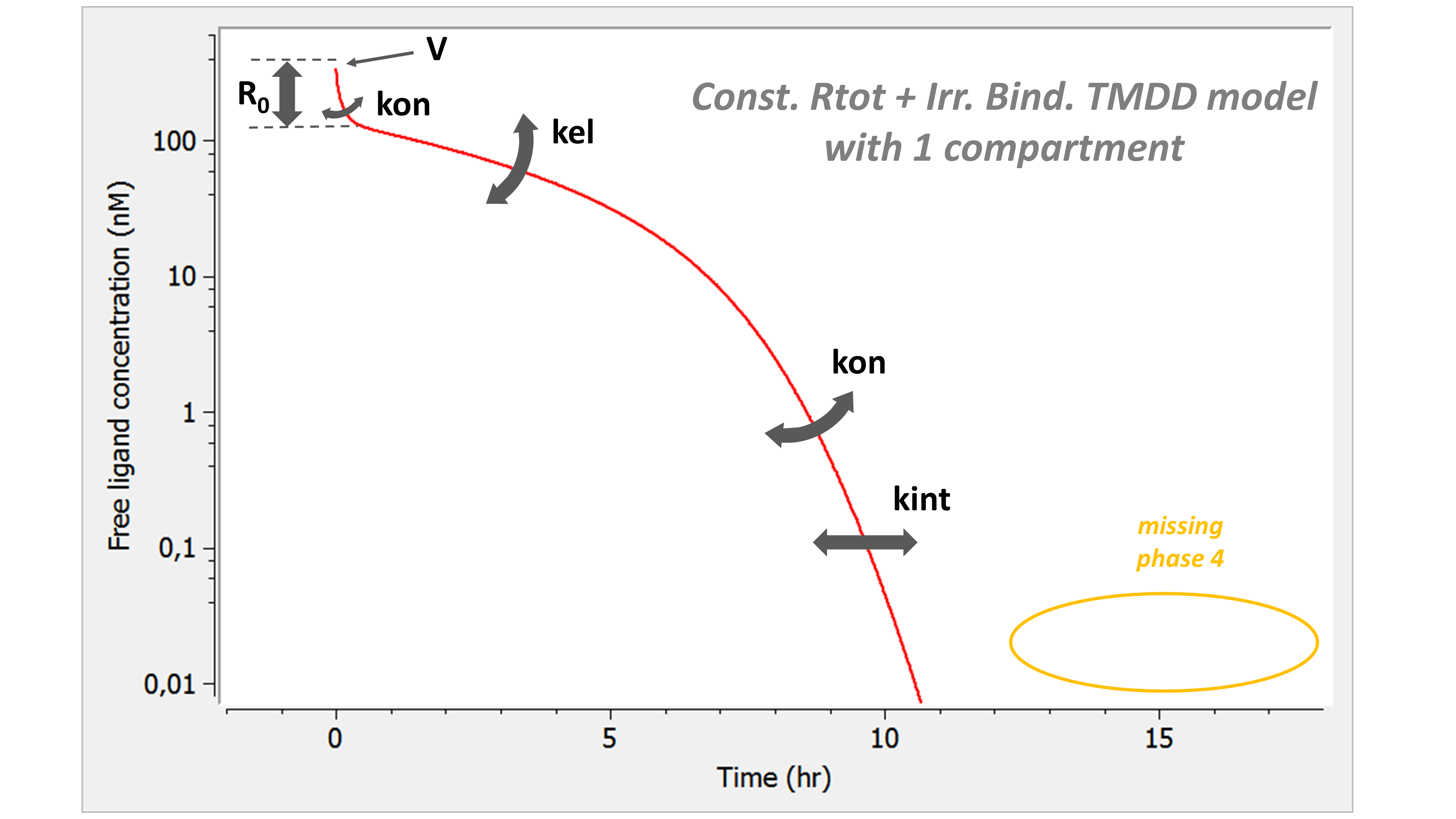
If one looks only at the free ligand concentration, this model is similar to the irreversible binding model. However it has one parameter less. Note that the phase 4 is missing.

Model with 2 compartments

If a second compartment is added, the shape is modified in the following way. Note that kon has been chosen large (very steep phase 1), to better focus on phase 2, where k12 and k21 have their main effect.

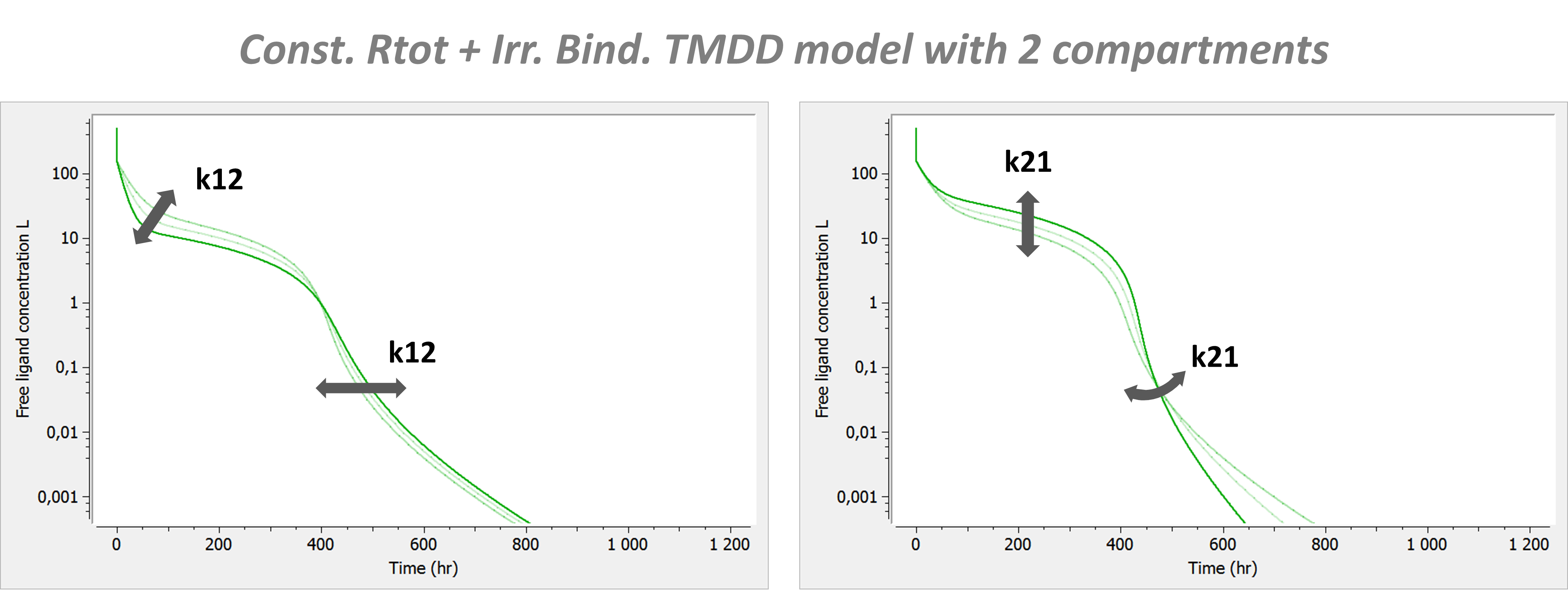
The introduction of a second compartment permits to recover a phase 4. Its flexibility is limited and linked to the effect of parameters k12 and k21 on phase 2.

Click here to go back to main TMDD page.

Detailed description of all the models